Shannon capacity, Lovász theta number and the Mycielski construction

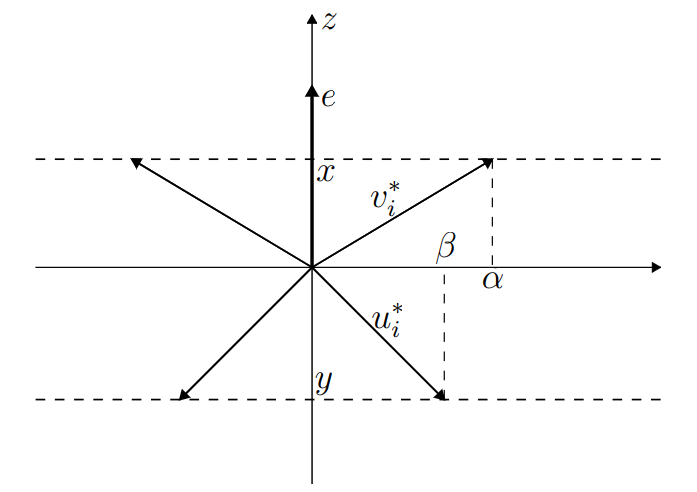
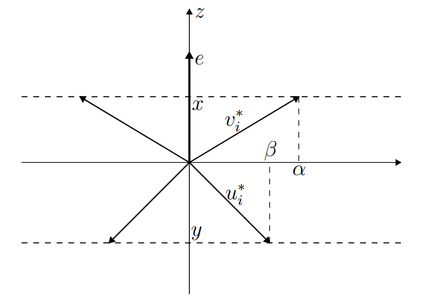
We investigate the effect of the well-known Mycielski construction on the Shannon capacity of graphs and on one of its most prominent upper bounds, the (complementary) Lov\'asz theta number. We prove that if the Shannon capacity of a graph, the distinguishability graph of a noisy channel, is attained by some finite power, then its Mycielskian has strictly larger Shannon capacity than the graph itself. For the complementary Lov\'asz theta function we show that its value on the Mycielskian of a graph is completely determined by its value on the original graph, a phenomenon similar to the one discovered for the fractional chromatic number by Larsen, Propp and Ullman. We also consider the possibility of generalizing our results on the Sperner capacity of directed graphs and on the generalized Mycielsky construction. Possible connections with what Zuiddam calls the asymptotic spectrum of graphs are discussed as well.