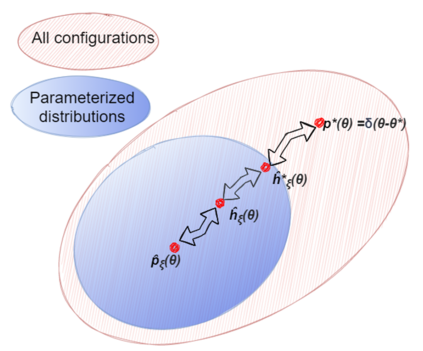
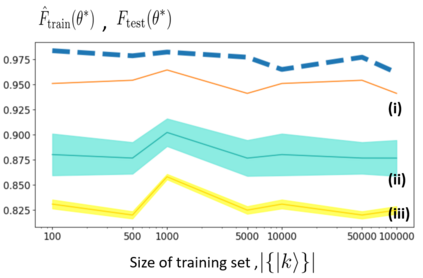
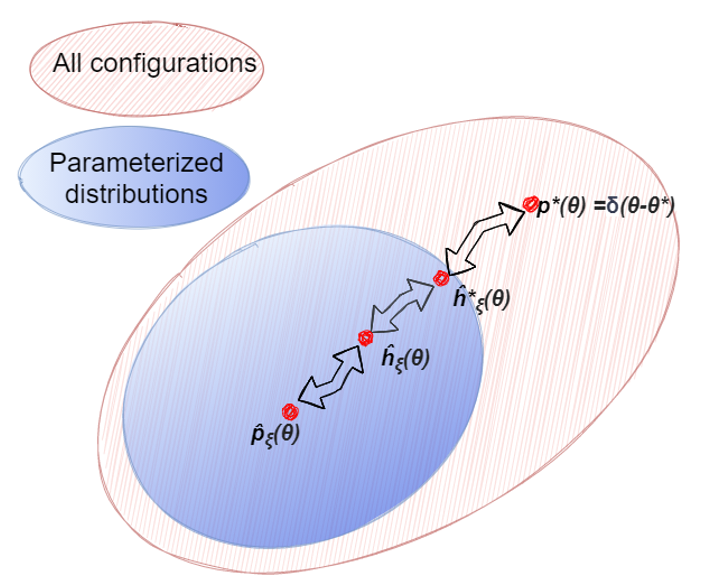
We propose a method for finding approximate compilations of quantum circuits, based on techniques from policy gradient reinforcement learning. The choice of a stochastic policy allows us to rephrase the optimization problem in terms of probability distributions, rather than variational parameters. This implies that searching for the optimal configuration is done by optimizing over the distribution parameters, rather than over the circuit free angles. The upshot of this is that we can always compute a gradient, provided that the policy is differentiable. We show numerically that this approach is more competitive than those using gradient-free methods, even in the presence of depolarizing noise, and argue analytically why this is the case. Another interesting feature of this approach to variational compilation is that it does not need a separate register and long-range interactions to estimate the end-point fidelity. We expect these techniques to be relevant for training variational circuit in other contexts
翻译:我们根据政策梯度强化学习的技术,建议一种寻找量子电路近似编集的方法。 选择一种随机政策,使我们能够用概率分布而不是变异参数来重新表述优化问题。 这意味着寻找最佳配置的方法是优化分布参数,而不是优化电路自由角度。 由此得出的结果是,只要政策是不同的,我们总是可以计算梯度。 我们从数字上表明,这一方法比使用无梯度方法的方法更具竞争力,即使在噪音分解的情况下也是如此,并且从分析角度来解释为什么是这样。 这种变异汇编方法的另一个有趣的特征是,它不需要单独的登记册和长距离互动来估计最终点的对等性。 我们期望这些技术与其他情况下的变异性电路培训有关。