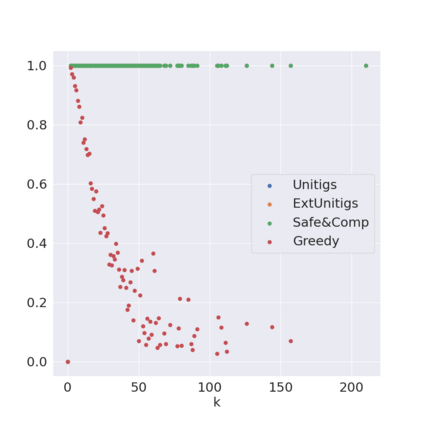
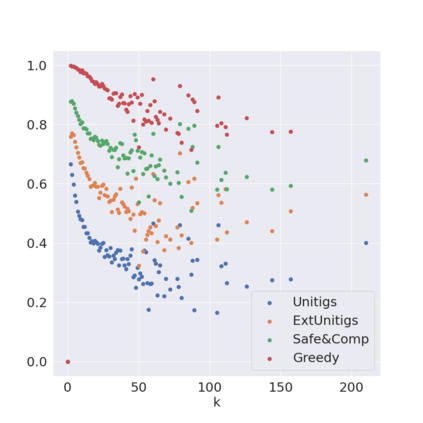
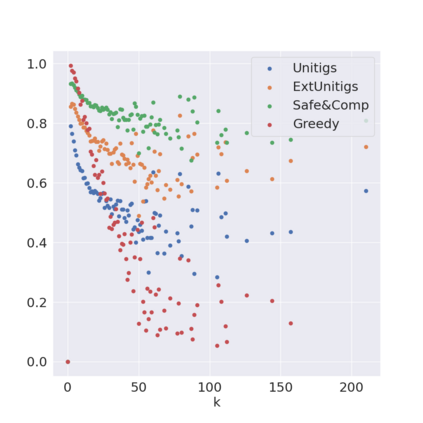
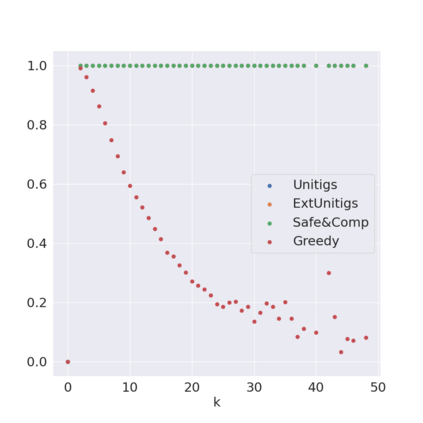
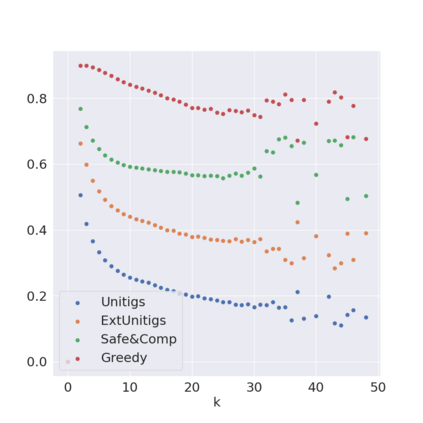
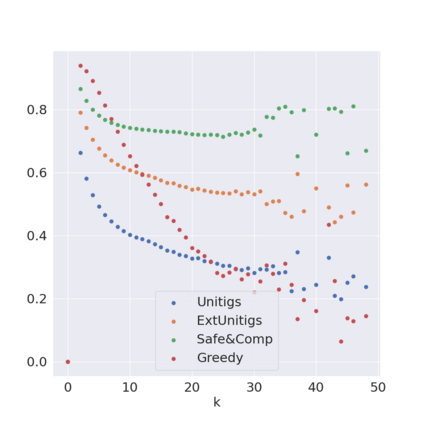
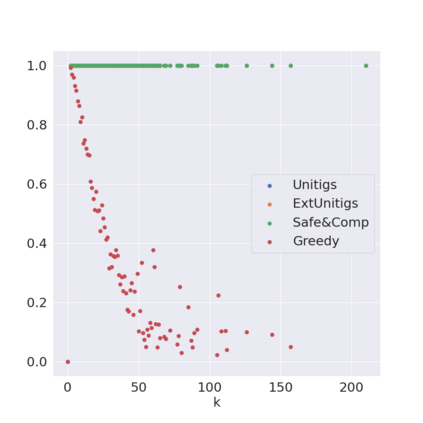
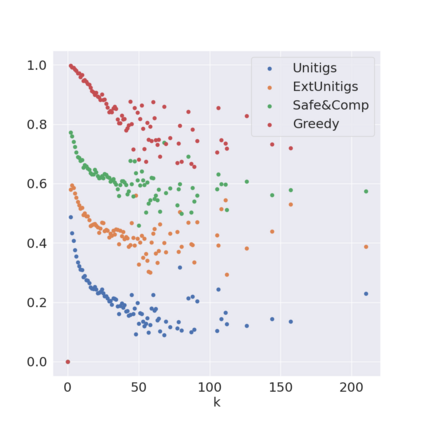
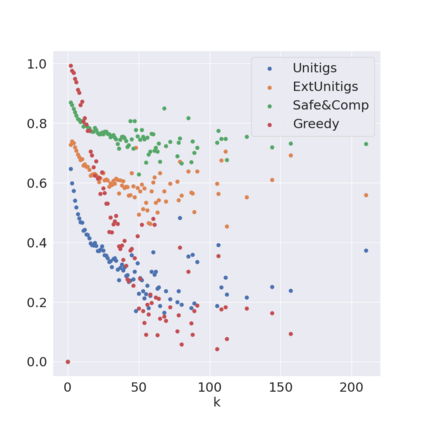
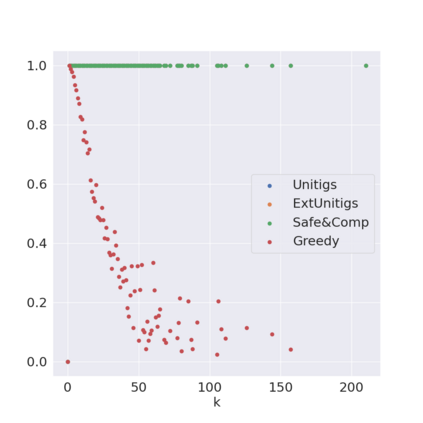
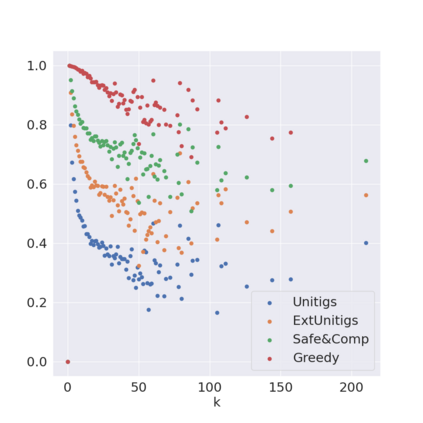
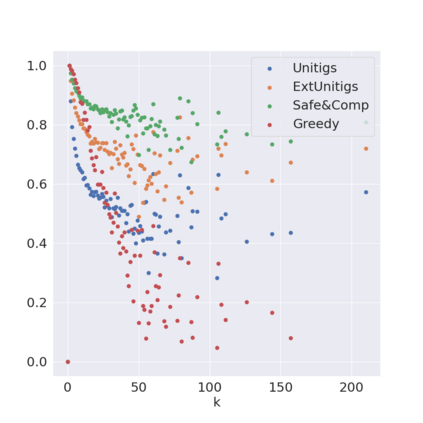
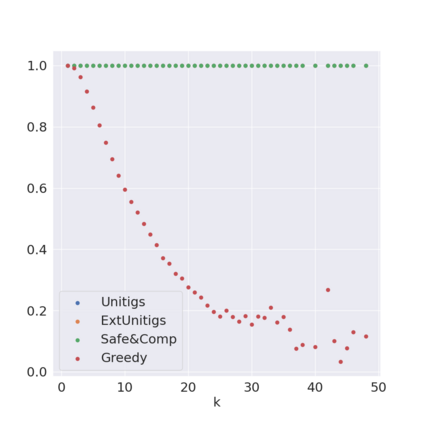
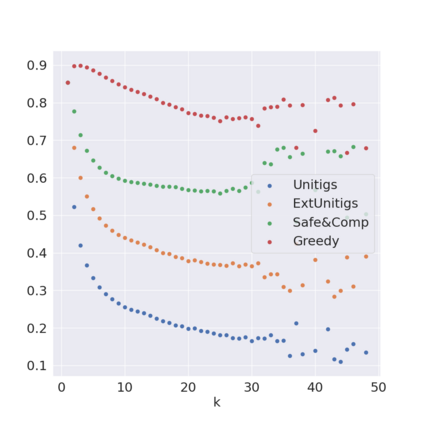
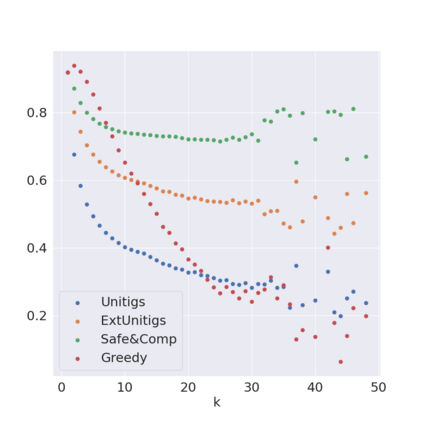
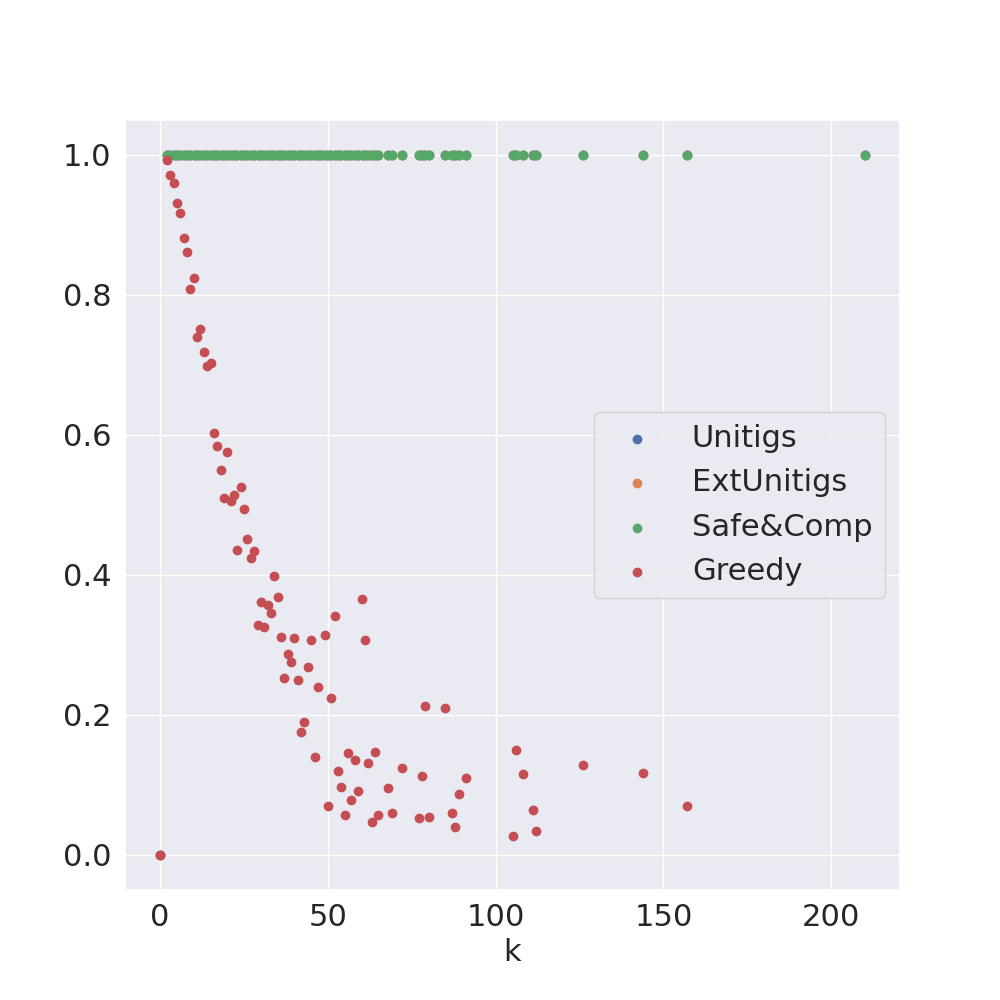
Decomposing a network flow into weighted paths has numerous applications. Some applications require any decomposition that is optimal w.r.t. some property such as number of paths, robustness, or length. Many bioinformatic applications require a specific decomposition where the paths correspond to some underlying data that generated the flow. For real inputs, no optimization criteria guarantees to uniquely identify the correct decomposition. Therefore, we propose to report safe paths, i.e., subpaths of at least one path in every flow decomposition. Ma, Zheng, and Kingsford [WABI 2020] addressed the existence of multiple optimal solutions in a probabilistic framework, i.e., non-identifiability. Later [RECOMB 2021], they gave a quadratic-time algorithm based on a global criterion for solving a problem called AND-Quant, which generalizes the problem of reporting whether a given path is safe. We give the first local characterization of safe paths for flow decompositions in directed acyclic graphs (DAGs), leading to a practical algorithm for finding the complete set of safe paths. We evaluated our algorithms against the trivial safe algorithms (unitigs, extended unitigs) and the popularly used heuristic (greedy-width) for flow decomposition on RNA transcripts datasets. Despite maintaining perfect precision our algorithm reports significantly higher coverage ($\approx 50\%$ more) than trivial safe algorithms. The greedy-width algorithm though reporting a better coverage, has significantly lower precision on complex graphs. Overall, our algorithm outperforms (by $\approx 20\%$) greedy-width on a unified metric (F-Score) when the dataset has significant number of complex graphs. Moreover, it has superior time ($3-5\times$) and space efficiency ($1.2-2.2\times$), resulting in a better and more practical approach for bioinformatics applications of flow decomposition.
翻译:将网络流分解为加权路径有许多应用程序。 有些应用程序需要任何最优化路径、 坚固度或长度等属性的分解。 许多生物信息应用程序需要特定的分解, 路径与生成流的某些基本数据相对应。 对于真实输入, 没有优化标准保证能独特识别正确的分解。 因此, 我们提议报告安全路径, 即每个流解分解至少一个路径的次路径。 Ma、 Zheng 和 Kingsford [WABI 2020] 解决了在概率框架( 即, 不可识别性) 中存在多个最佳解决方案。 许多生物信息应用程序需要特定的分解。 之后 [ReCOMB 20211], 它们给出了基于解决一个被称作 AND- Qunatiot 的问题的全球标准的二次算法。 因此, 我们建议报告安全路径是否安全。 我们第一次对复杂路径的解析( 美元- complioalityalityalation) 进行本地分解调( DAGAG), 导致一个实际的更精确的更精确的解算算法, 虽然我们使用了更精确的直径直径的代数据。