Parameterized Algorithms for the Steiner Tree Problem on a Directed Hypercube

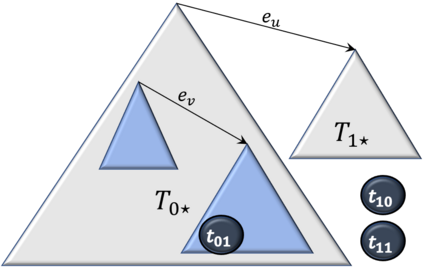
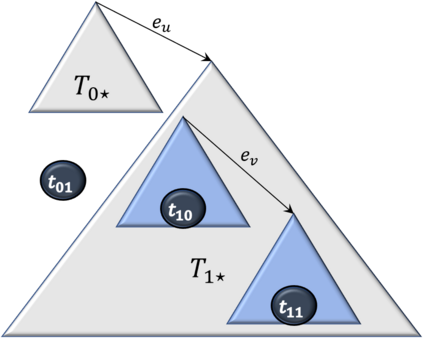
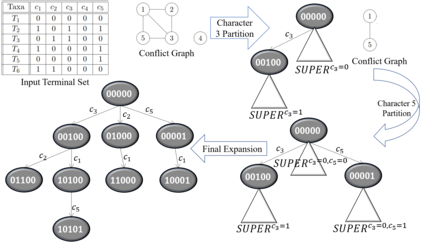
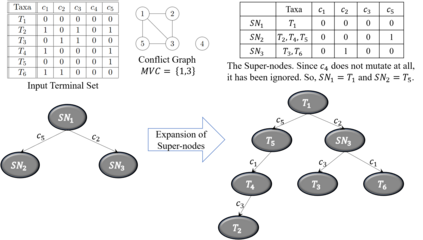
We address the problem of computing a Steiner Arborescence on a directed hypercube. The directed hypercube enjoys a special connectivity structure among its node set $\{0,1\}^m$, but its exponential in $m$ size renders traditional Steiner tree algorithms inefficient. Even though the problem was known to be NP-complete, parameterized complexity of the problem was unknown. With applications in evolutionary tree reconstruction algorithms and incremental algorithms for computing a property on multiple input graphs, any algorithm for this problem would open up new ways to study these applications. In this paper, we present the first algorithms, to the best our knowledge, that prove the problem to be fixed parameter tractable (FPT) wrt two natural parameters -- number of input terminals and penalty of the arborescence. Given any directed $m$-dimensional hypercube, rooted at the zero node, and a set of input terminals $R$ that needs to be spanned by the Steiner arborescence, we prove that the problem is FPT wrt the penalty parameter $q$, by providing a randomized algorithm that computes an optimal arborescence $T$ in $O\left(q^44^{q\left(q+1\right)}+q\left|R\right|m^2\right)$ with probability at least $4^{-q}$. If we trade-off exact solution for an additive approximate one, then we can design a parameterized approximation algorithm with better running time - computing an arborescence $T$ with cost at most $OPT+(\left|R\right|-4)(q_{opt}-1)$ in time $O(\left|R\right|m^2+1.2738^{q_{opt}})$. We also present a dynamic programming algorithm that computes an optimal arborescence in $O(3^{\left|R\right|}\left|R\right|m)$ time, thus proving that the problem is FPT on the parameter $\left|R\right|$.