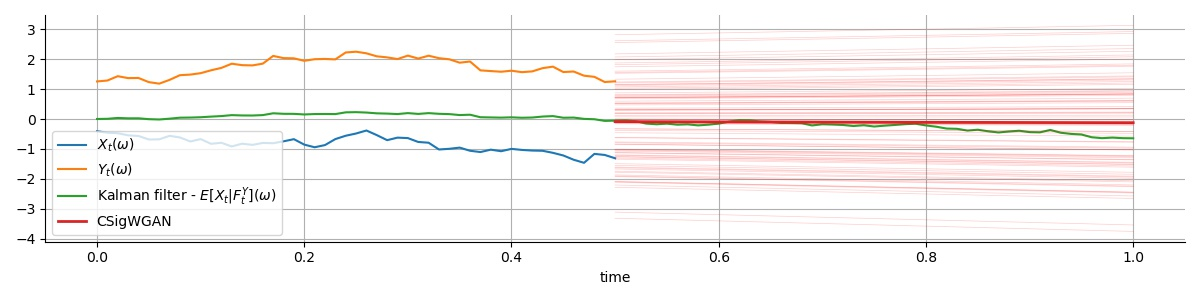
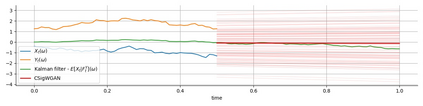
We consider the filtering and prediction problem for a diffusion process. The signal and observation are modeled by stochastic differential equations (SDEs) driven by correlated Wiener processes. In classical estimation theory, measure-valued stochastic partial differential equations (SPDEs) are derived for the filtering and prediction measures. These equations can be hard to solve numerically. We provide an approximation algorithm using conditional generative adversarial networks (GANs) in combination with signatures, an object from rough path theory. The signature of a sufficiently smooth path determines the path completely. As a result, in some cases, GANs based on signatures have been shown to efficiently approximate the law of a stochastic process. For our algorithm we extend this method to sample from the conditional law, given noisy, partial observation. Our generator is constructed using neural differential equations (NDEs), relying on their universal approximator property. We show well-posedness in providing a rigorous mathematical framework. Numerical results show the efficiency of our algorithm.
翻译:我们认为过滤和预测是扩散过程的问题。 信号和观察是由维纳进程相关驱动的随机差分方程式( SDEs) 模拟的。 在古典估计理论中, 过滤和预测措施的计算法是量值的随机差分方程(SPDEs) 。 这些方程很难用数字来解析。 我们使用条件的基因对抗网络(GANs) 提供近似算法, 加上签名, 这是来自粗路径理论的一个对象。 足够顺利路径的签名可以完全决定路径。 结果, 在某些情况下, 基于签名的GANs 被显示有效接近了随机进程的法律。 对于我们的算法, 我们的算法将这一方法扩展为有条件法律的样本, 由于噪音和部分观察。 我们的生成方程式是使用神经差方程(NDEs) 构建的, 并依靠其通用的亚化方程特性。 我们在提供严格的数学框架时表现出很好的定位。 数字结果显示我们的算法的效率。