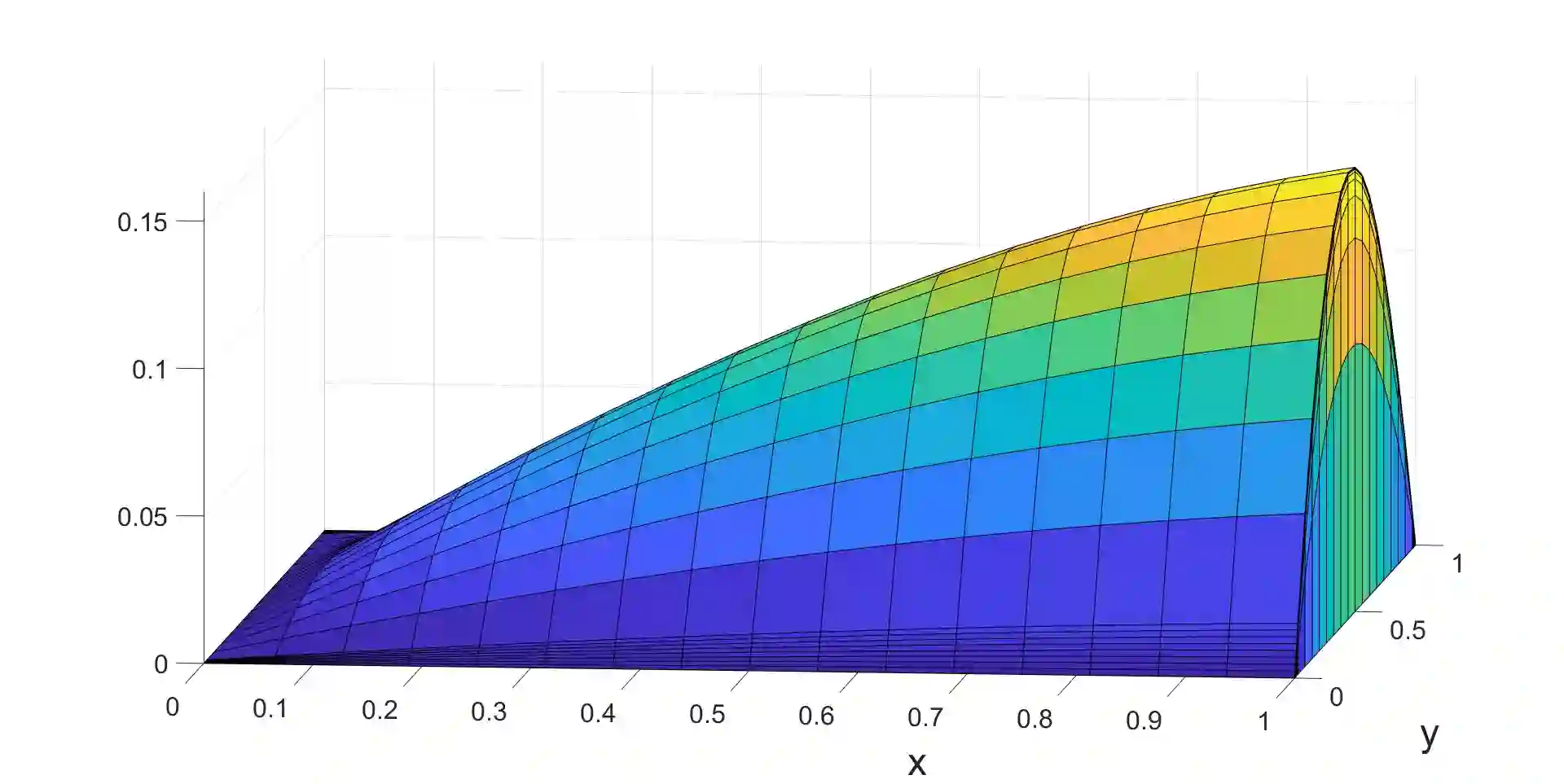
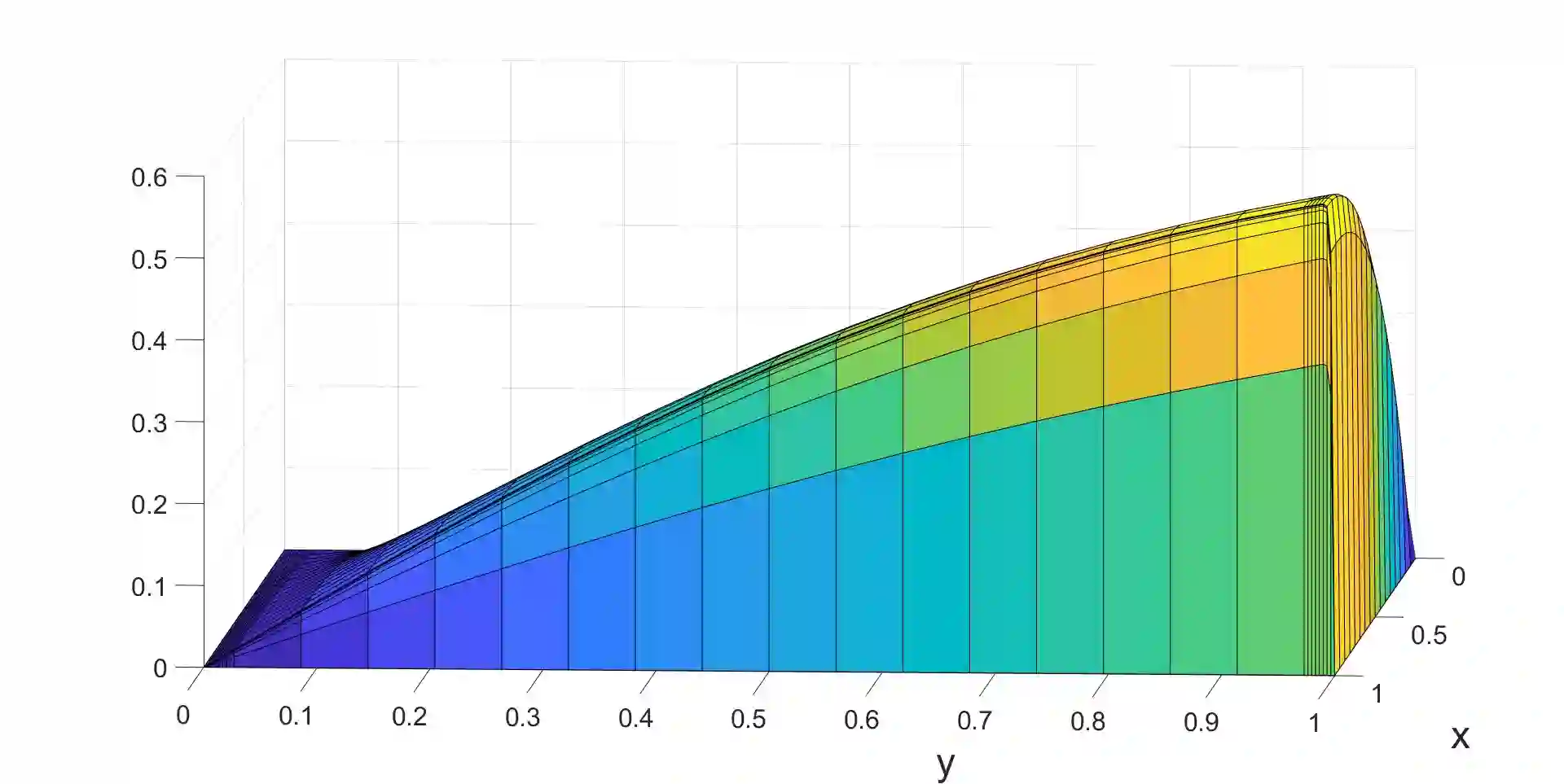
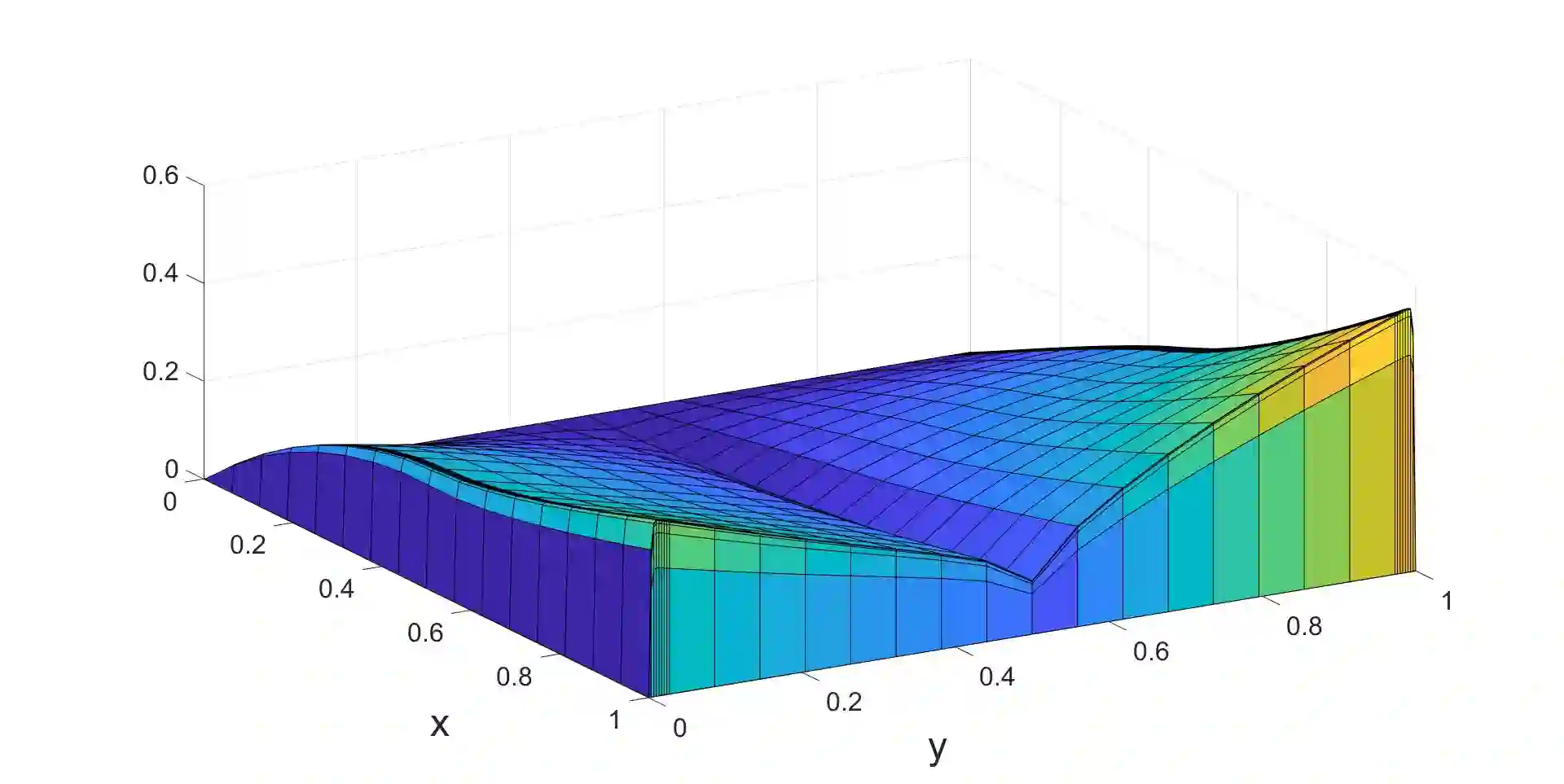
A Petrov-Galerkin finite element method is constructed for a singularly perturbed elliptic problem in two space dimensions. The solution contains a regular boundary layer and two characteristic boundary layers. Exponential splines are used as test functions in one coordinate direction and are combined with bilinear trial functions defined on a Shishkin mesh. The resulting numerical method is shown to be a stable parameter-uniform numerical method that achieves a higher order of convergence compared to upwinding on the same mesh.
翻译:暂无翻译
相关内容
专知会员服务
54+阅读 · 2020年1月30日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2023年12月19日
Arxiv
0+阅读 · 2023年12月19日
Arxiv
0+阅读 · 2023年12月18日
Arxiv
0+阅读 · 2023年12月15日