Support Recovery in Universal One-bit Compressed Sensing

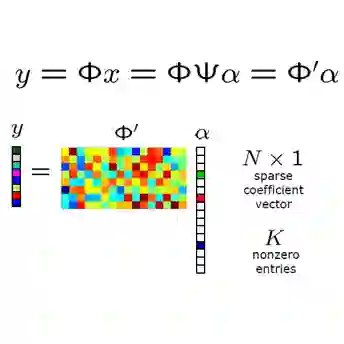
One-bit compressed sensing (1bCS) is an extreme-quantized signal acquisition method that has been widely studied in the past decade. In 1bCS, linear samples of a high dimensional signal are quantized to only one bit per sample (sign of the measurement). Assuming the original signal vector to be sparse, existing results either aim to find the support of the vector, or approximate the signal within an $\epsilon$-ball. The focus of this paper is support recovery, which often also computationally facilitates approximate signal recovery. A universal measurement matrix for 1bCS refers to one set of measurements that work for all sparse signals. With universality, it is known that $\tilde{\Theta}(k^2)$ 1bCS measurements are necessary and sufficient for support recovery (where $k$ denotes the sparsity). In this work, we show that it is possible to universally recover the support with a small number of false positives with $\tilde{O}(k^{3/2})$ measurements. If the dynamic range of the signal vector is known, then with a different technique, this result can be improved to only $\tilde{O}(k)$ measurements. Further results on support recovery are also provided.