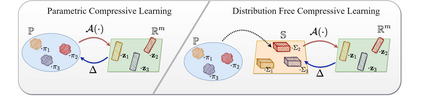
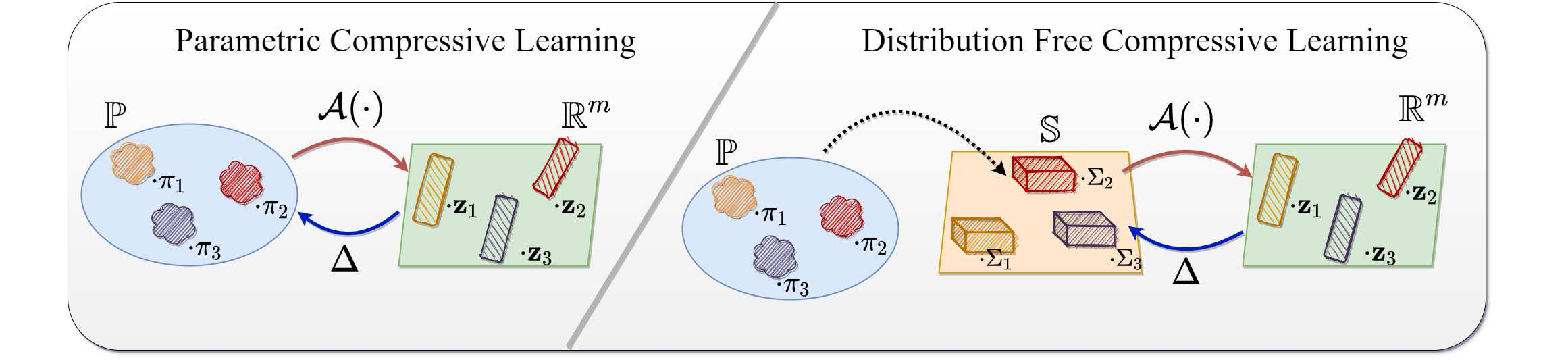
Compressive learning forms the exciting intersection between compressed sensing and statistical learning where one exploits forms of sparsity and structure to reduce the memory and/or computational complexity of the learning task. In this paper, we look at the independent component analysis (ICA) model through the compressive learning lens. In particular, we show that solutions to the cumulant based ICA model have particular structure that induces a low dimensional model set that resides in the cumulant tensor space. By showing a restricted isometry property holds for random cumulants e.g. Gaussian ensembles, we prove the existence of a compressive ICA scheme. Thereafter, we propose two algorithms of the form of an iterative projection gradient (IPG) and an alternating steepest descent (ASD) algorithm for compressive ICA, where the order of compression asserted from the restricted isometry property is realised through empirical results. We provide analysis of the CICA algorithms including the effects of finite samples. The effects of compression are characterised by a trade-off between the sketch size and the statistical efficiency of the ICA estimates. By considering synthetic and real datasets, we show the substantial memory gains achieved over well-known ICA algorithms by using one of the proposed CICA algorithms. Finally, we conclude the paper with open problems including interesting challenges from the emerging field of compressive learning.
翻译:压缩感测和统计学习之间令人兴奋的压缩感应和统计学习交叉形式,在其中,人们利用多种形式的宽度和结构来减少学习任务的记忆和/或计算复杂性。在本文中,我们通过压缩学习镜头来查看独立组成部分分析模型(ICA),特别是,我们表明,基于累积的ICA模型的解决方案有特殊的结构,产生一个位于累积的振幅空间的低维模型集。我们通过显示随机蓄积物(例如高斯安组装)的限量异度属性,我们证明存在压缩的ICA方案。之后,我们提出了两种关于迭代预测梯度(IPG)形式和压缩缩缩放式最陡度(ASD)计算法的算法,在这种结构中,通过实验结果可以实现从限制的偏差的偏差的偏差性模型组合。我们分析了CAA的算法对随机蓄积物的量和统计效率进行了权衡。最后,我们用CAA的深度的模型算法总结了我们从CAAA的深度和最新测算法中取得了哪些成果。