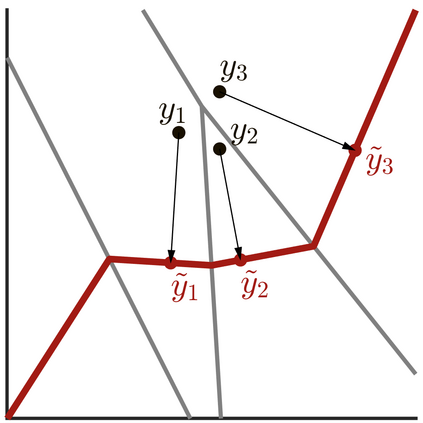
We analyze neural networks composed of bijective flows and injective expansive elements. We find that such networks universally approximate a large class of manifolds simultaneously with densities supported on them. Among others, our results apply to the well-known coupling and autoregressive flows. We build on the work of Teshima et al. 2020 on bijective flows and study injective architectures proposed in Brehmer et al. 2020 and Kothari et al. 2021. Our results leverage a new theoretical device called the embedding gap, which measures how far one continuous manifold is from embedding another. We relate the embedding gap to a relaxation of universally we call the manifold embedding property, capturing the geometric part of universality. Our proof also establishes that optimality of a network can be established in reverse, resolving a conjecture made in Brehmer et al. 2020 and opening the door for simple layer-wise training schemes. Finally, we show that the studied networks admit an exact layer-wise projection result, Bayesian uncertainty quantification, and black-box recovery of network weights.
翻译:我们分析由双向流动和导射扩展元素组成的神经网络。 我们发现,这种网络普遍与大量多层的多层相近,同时支持密度。 我们的结果适用于众所周知的联结和自动递减流。 我们以Teshima等人2020年在Brehmer等人(2020年)和Kothari等人(2021年)提出的双向流和预测性结构方面开展的工作为基础,在Teshima等人2020年关于双向流动和研究双向流和预测性结构的工作的基础上再接再厉。 我们的结果利用了一个新的理论装置,称为嵌入差距,它测量一个连续的元体离嵌入另一个元体有多远。我们把嵌入的鸿沟与我们普遍称为多层嵌入属性的放松联系起来,捕捉到普遍性的几何部分。我们的证据还证明,一个网络的最佳性可以建立反向,解决在Brehmer等人(2020年)和Kothari等人(Kothari)等人(Kothari)等人(2021年)提出的预测。 我们的结果表明,所研究的网络接受了一种精确的层次预测结果,即Bayesian不确定性的量化和黑箱网络重量的回收。