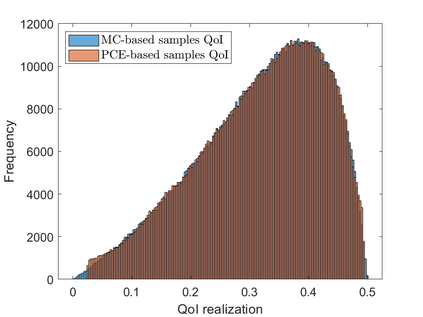
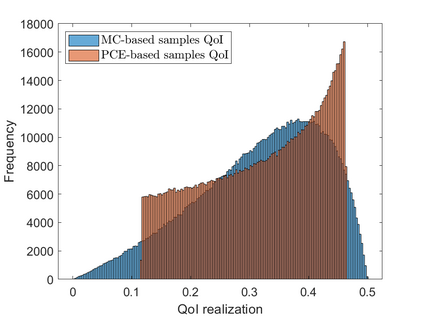
We are concerned with random ordinary differential equations (RODEs). Our main question of interest is how uncertainties in system parameters propagate through the possibly highly nonlinear dynamical system and affect the system's bifurcation behavior. We come up with a methodology to determine the probability of the occurrence of different types of bifurcations (sub- vs super-critical) along a given bifurcation curve based on the probability distribution of the input parameters. In a first step, we reduce the system's behavior to the dynamics on its center manifold. We thereby still capture the major qualitative behavior of the RODEs. In a second step, we analyze the reduced RODEs and quantify the probability of the occurrence of different types of bifurcations based on the (nonlinear) functional appearance of uncertain parameters. To realize this major step, we present three approaches: an analytical one, where the probability can be calculated explicitly based on Mellin transformation and inversion, a semi-analytical one consisting of a combination of the analytical approach with a moment-based numerical estimation procedure, and a particular sampling-based approach using unscented transformation. We complement our new methodology with various numerical examples.
翻译:我们关心的是随机的普通差异方程式。 我们关心的主要问题是,系统参数的不确定性是如何通过可能高度非线性动态系统传播的,如何影响系统的双向行为。 我们想出一种方法,根据输入参数的概率分布,沿着一个特定的双向曲线,确定不同类型双向(子对超临界)的发生概率。 第一步,我们将系统的行为降低到其中心方形的动态。 因此,我们仍能捕捉到RODE的主要定性行为。 第二步,我们根据(非线性)参数的功能外观,分析减少的RODE并量化不同类型双向的发生概率。为了实现这一重大步骤,我们提出三种方法:分析方法,其中可以明确根据Mellin的变换和反向计算概率,半分析方法,包括将分析方法与基于瞬间的数字估计程序相结合,以及使用非点性变法的具体抽样方法。我们用新的数字方法补充了我们的各种数字示例。