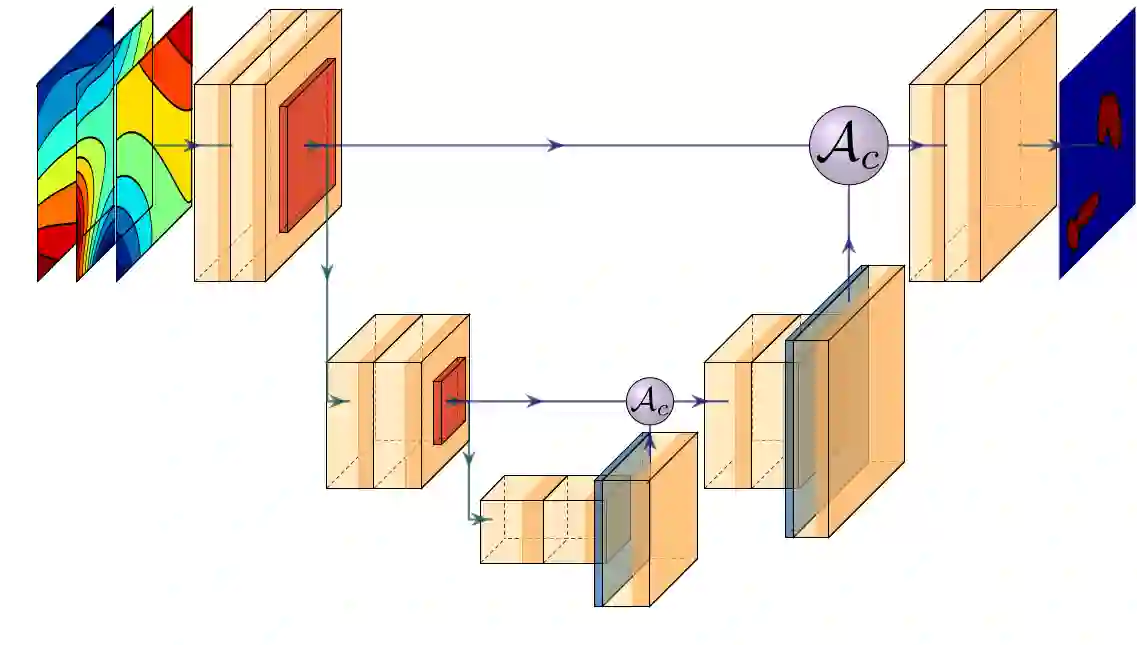
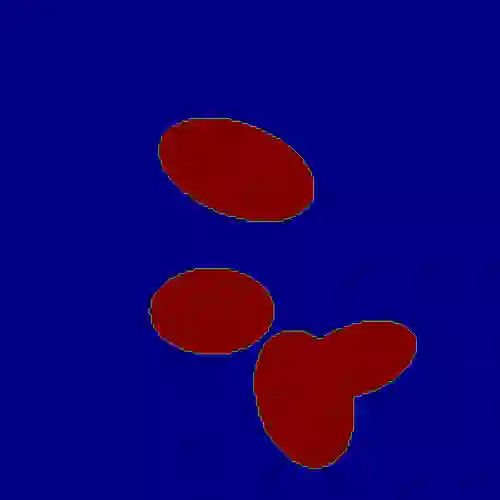
A Transformer-based deep direct sampling method is proposed for a class of boundary value inverse problems. A real-time reconstruction is achieved by evaluating the learned inverse operator between carefully designed data and the reconstructed images. An effort is made to give a specific example to a fundamental question: whether and how one can benefit from the theoretical structure of a mathematical problem to develop task-oriented and structure-conforming deep neural networks? Specifically, inspired by direct sampling methods for inverse problems, the 1D boundary data in different frequencies are preprocessed by a partial differential equation-based feature map to yield 2D harmonic extensions as different input channels. Then, by introducing learnable non-local kernels, the direct sampling is recast to a modified attention mechanism. The proposed method is then applied to electrical impedance tomography, a well-known severely ill-posed nonlinear inverse problem. The new method achieves superior accuracy over its predecessors and contemporary operator learners, as well as shows robustness with respect to noise. This research shall strengthen the insights that the attention mechanism, despite being invented for natural language processing tasks, offers great flexibility to be modified in conformity with the a priori mathematical knowledge, which ultimately leads to the design of more physics-compatible neural architectures.
翻译:为一组边界值反向问题提议了一个基于变压器的深深深直接取样方法。通过对经过仔细设计的数据和经过重建的图像之间所学的反向操作器进行评估,可以实现实时重建。然后,通过引入可学习的非本地内核,将直接取样重新排入一个修改的注意机制。然后,将拟议方法应用于一个根本问题:数学问题的理论结构是否以及如何从中得益,以开发以任务为导向的、结构与结构相符的深神经网络?具体地说,在对反向问题直接取样方法的启发下,不同频率的1D边界数据通过一个部分差异方程式图进行预处理,以产生2D相容扩展作为不同的输入渠道。然后,通过引入可学习的非本地内核器,直接取样被重新排入到一个经过修改的注意机制。然后,拟议方法将被用于一个众所周知的严重错误的、与结构不相适应的数学问题。新方法比其前身和当代操作者学习者更精确,并显示对噪音的坚韧性。这项研究将加强人们的认识,即注意机制尽管被发明用于自然语言处理任务,但最终会修改为符合数学结构。