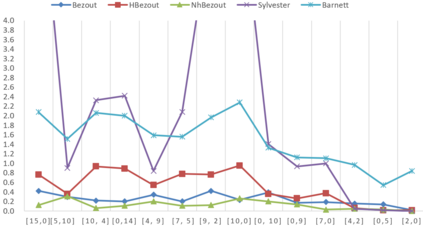
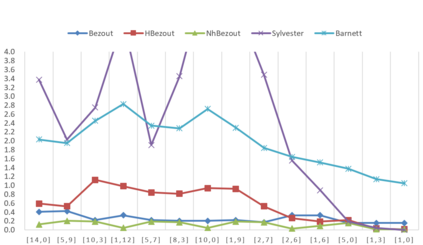
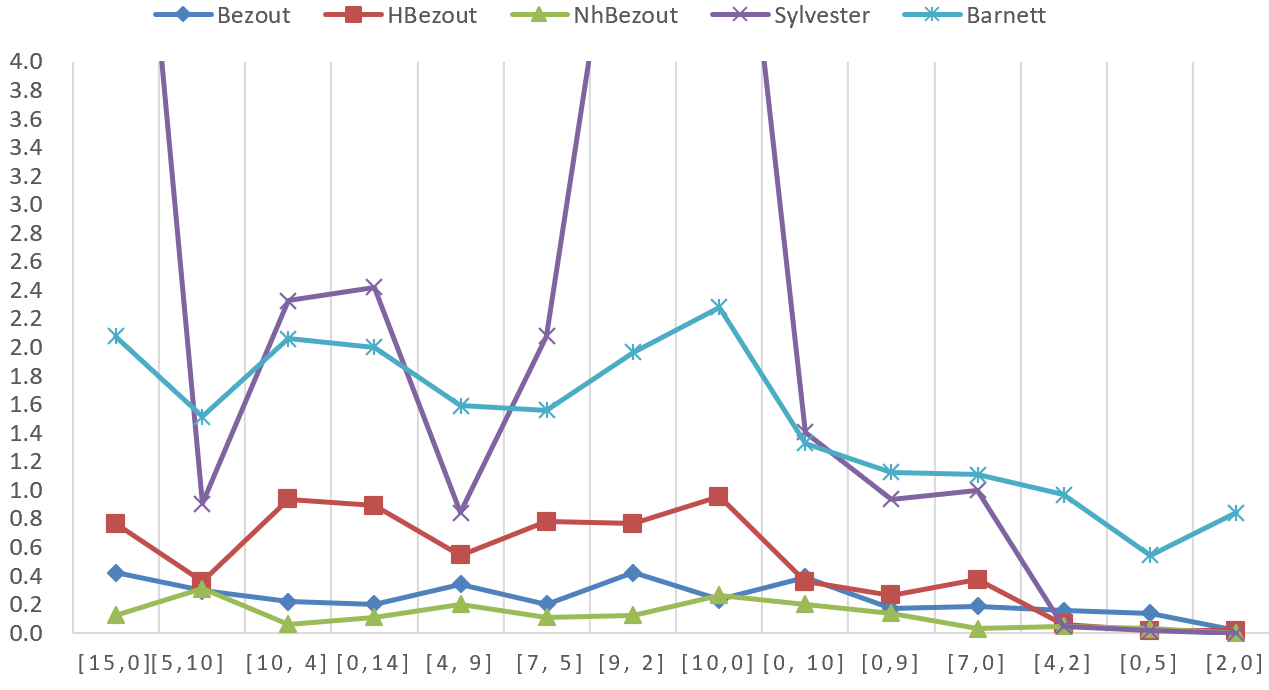
In this paper, we develop two variants of Bezout subresultant formulas for several polynomials, i.e., hybrid Bezout subresultant polynomial and non-homogeneous Bezout subresultant polynomial. Rather than simply extending the variants of Bezout subresultant formulas developed by Diaz-Toca and Gonzalez-Vega in 2004 for two polynomials to arbitrary number of polynomials, we propose a new approach to formulating two variants of the Bezout-type subresultant polynomials for a set of univariate polynomials. Experimental results show that the Bezout-type subresultant formulas behave better than other known formulas when used to compute multi-polynomial subresultants, among which the non-homogeneous Bezout-type formula shows the best performance.
翻译:暂无翻译