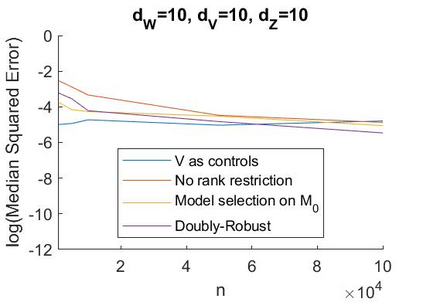
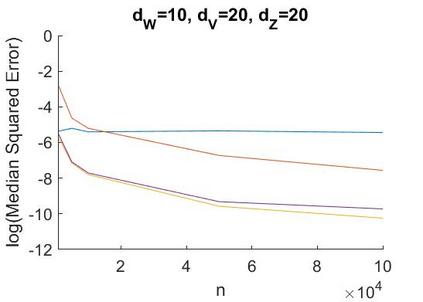
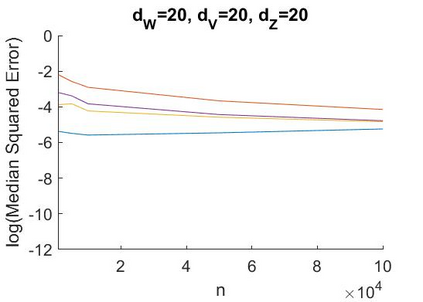
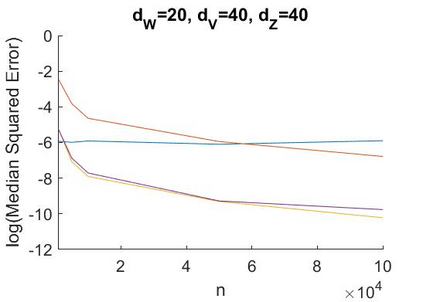
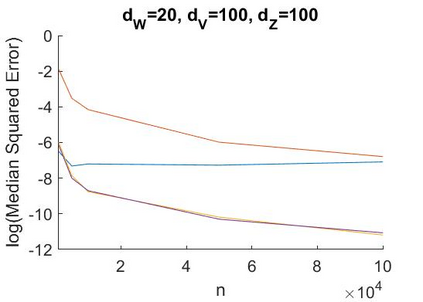
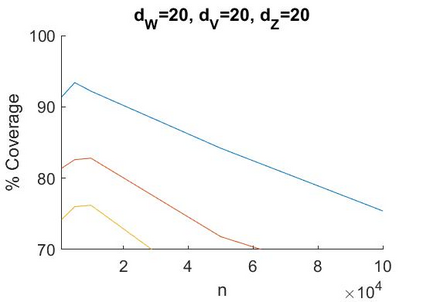
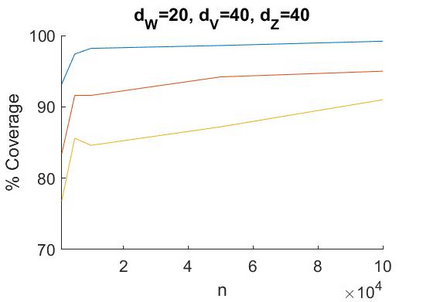
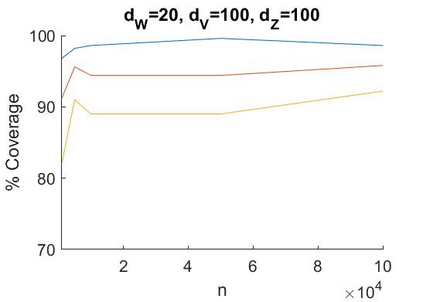
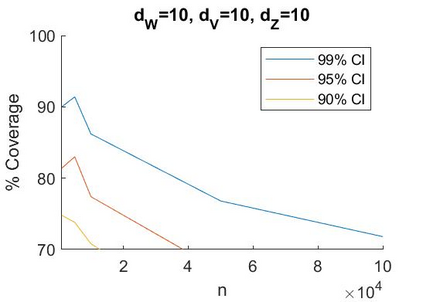
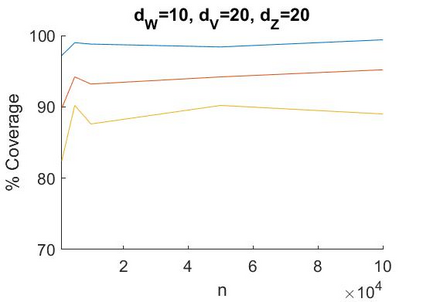
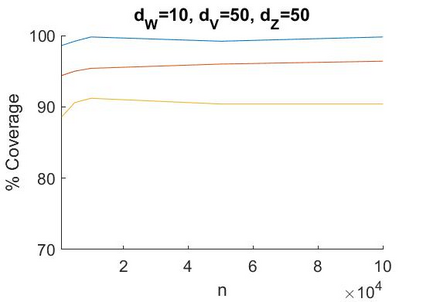
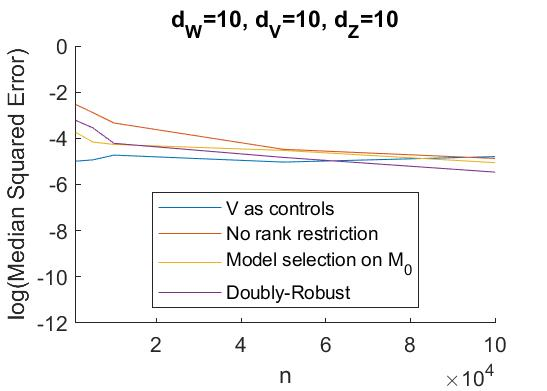
A recent literature considers causal inference using noisy proxies for unobserved confounding factors. The proxies are divided into two sets that are independent conditional on the confounders. One set of proxies are `negative control treatments' and the other are `negative control outcomes'. Existing work applies to low-dimensional settings with a fixed number of proxies and confounders. In this work we consider linear models with many proxy controls and possibly many confounders. A key insight is that if each group of proxies is strictly larger than the number of confounding factors, then a matrix of nuisance parameters has a low-rank structure and a vector of nuisance parameters has a sparse structure. We can exploit the rank-restriction and sparsity to reduce the number of free parameters to be estimated. The number of unobserved confounders is not known a priori but we show that it is identified, and we apply penalization methods to adapt to this quantity. We provide an estimator with a closed-form as well as a doubly-robust estimator that must be evaluated using numerical methods. We provide conditions under which our doubly-robust estimator is uniformly root-$n$ consistent, asymptotically centered normal, and our suggested confidence intervals have asymptotically correct coverage. We provide simulation evidence that our methods achieve better performance than existing approaches in high dimensions, particularly when the number of proxies is substantially larger than the number of confounders.
翻译:最近的一个文献认为,对于未观察到的周期性折叠因素,使用噪音的杂交来计算因果推断。代理人分为两组,两组以混杂因素为独立条件。一组替代物为“负控制处理”,另一组为“负控制结果”。现有的工作适用于低维设置,有固定数量的代理人和混杂者。在这项工作中,我们考虑的线性模型有许多代用控制器,而且可能有许多混杂因素。一个关键的见解是,如果每组代理人严格大于相纠结因素的数量,那么,一个较复杂的参数矩阵则具有低级结构,而一个含混杂参数的矢量则结构稀少。我们可以利用等级限制和宽度来减少要估计的自由参数的数量。未观察到的粘结者的数量并不为人所熟,但我们发现,我们采用惩罚性数字的方法来适应这个数量。我们提供一个封闭式的缩略图,一个较封闭的缩略图,而且覆盖范围的矩阵结构结构结构更低,而一个含混杂因素的矢测值参数结构结构结构结构结构则很少。我们可以利用等级-直观性地评估我们现有的精确度方法,而必须提供我们目前的平定的计算方法。