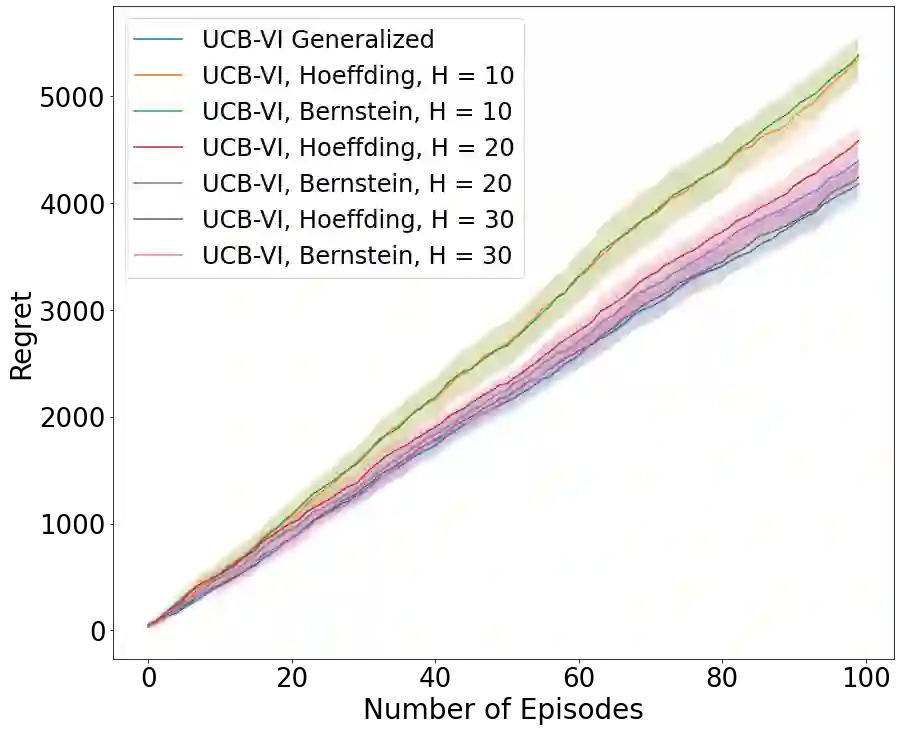
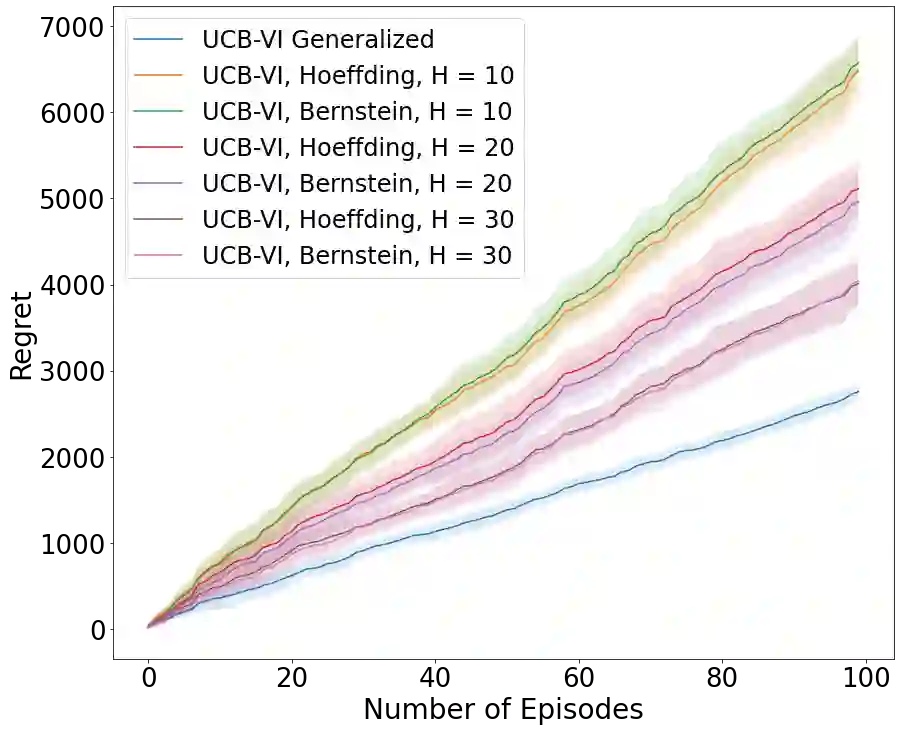
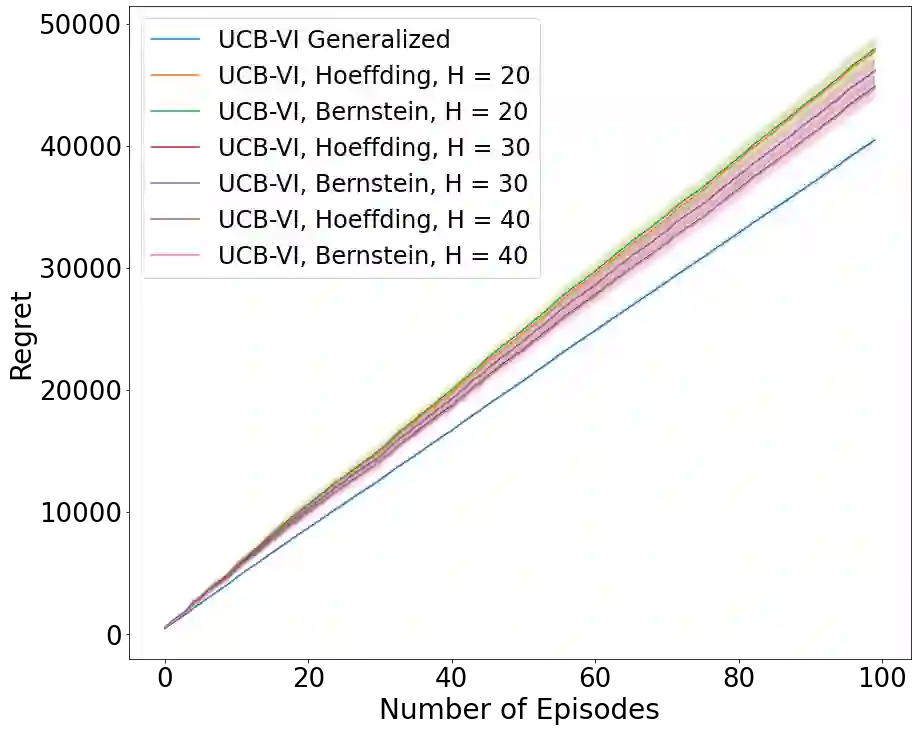
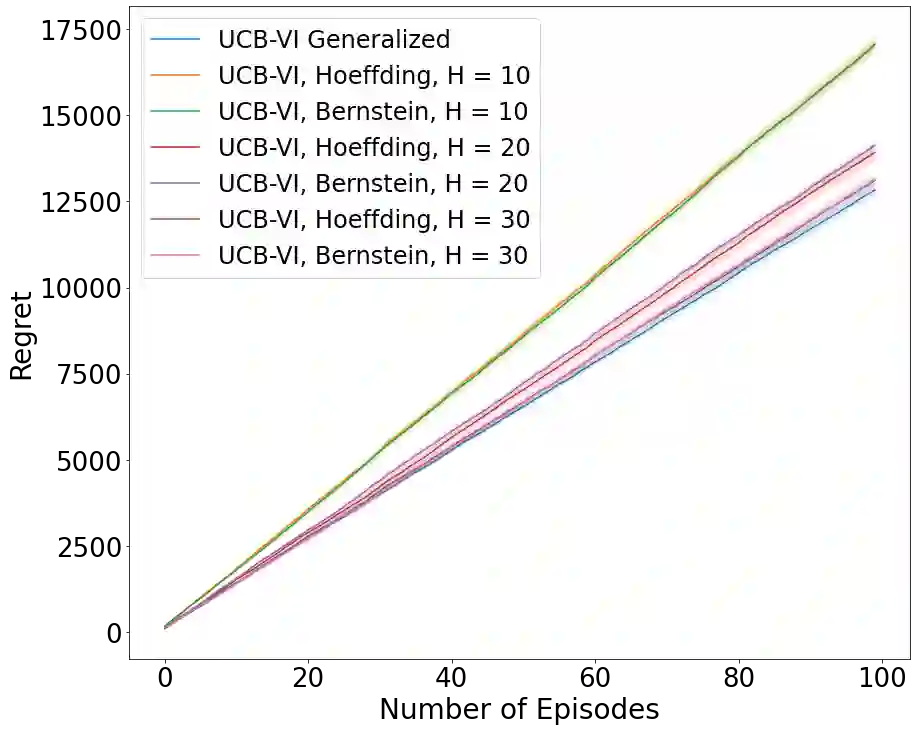
Existing episodic reinforcement algorithms assume that the length of an episode is fixed across time and known a priori. In this paper, we consider a general framework of episodic reinforcement learning when the length of each episode is drawn from a distribution. We first establish that this problem is equivalent to online reinforcement learning with general discounting where the learner is trying to optimize the expected discounted sum of rewards over an infinite horizon, but where the discounting function is not necessarily geometric. We show that minimizing regret with this new general discounting is equivalent to minimizing regret with uncertain episode lengths. We then design a reinforcement learning algorithm that minimizes regret with general discounting but acts for the setting with uncertain episode lengths. We instantiate our general bound for different types of discounting, including geometric and polynomial discounting. We also show that we can obtain similar regret bounds even when the uncertainty over the episode lengths is unknown, by estimating the unknown distribution over time. Finally, we compare our learning algorithms with existing value-iteration based episodic RL algorithms in a grid-world environment.
翻译:现有的单数加固算法假定一个事件的时间长度在时间上是固定的,已知的先验性。 在本文中, 当每个事件的时间长度从分布中抽取时, 我们考虑一个常数加固学习的一般框架。 我们首先确定, 这个问题相当于在线加固学习, 并给予一般折扣, 因为学习者试图在无限的地平线上优化预期的折扣奖励金额, 但贴现功能不一定具有几何性。 我们显示, 以这种新的一般折扣来尽量减少遗憾, 等于以不确定的序段长度来尽量减少遗憾。 然后我们设计一个加固学习算法, 以一般折扣来尽量减少遗憾, 但以不确定的序段长度为设定动作。 我们即时将一般的折扣绑在不同的类型上, 包括几何和多元折扣上。 我们还表明, 即使在时间长度的不确定性未知时, 我们也可以通过估计未知的时段分布来获得类似的遗憾界限。 最后, 我们把学习算法与基于现有价值的子分化 RL 算法进行比较 。