Asymptotic Independence of the Sum and Maximum of Dependent Random Variables with Applications to High-Dimensional Tests

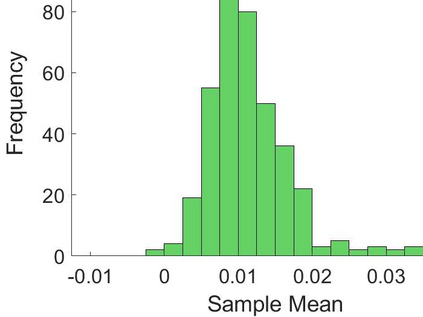
For a set of dependent random variables, without stationary or the strong mixing assumptions, we derive the asymptotic independence between their sums and maxima. Then we apply this result to high-dimensional testing problems, where we combine the sum-type and max-type tests and propose a novel test procedure for the one-sample mean test, the two-sample mean test and the regression coefficient test in high-dimensional setting. Based on the asymptotic independence between sums and maxima, the asymptotic distributions of test statistics are established. Simulation studies show that our proposed tests have good performance regardless of data being sparse or not. Examples on real data are also presented to demonstrate the advantages of our proposed methods.