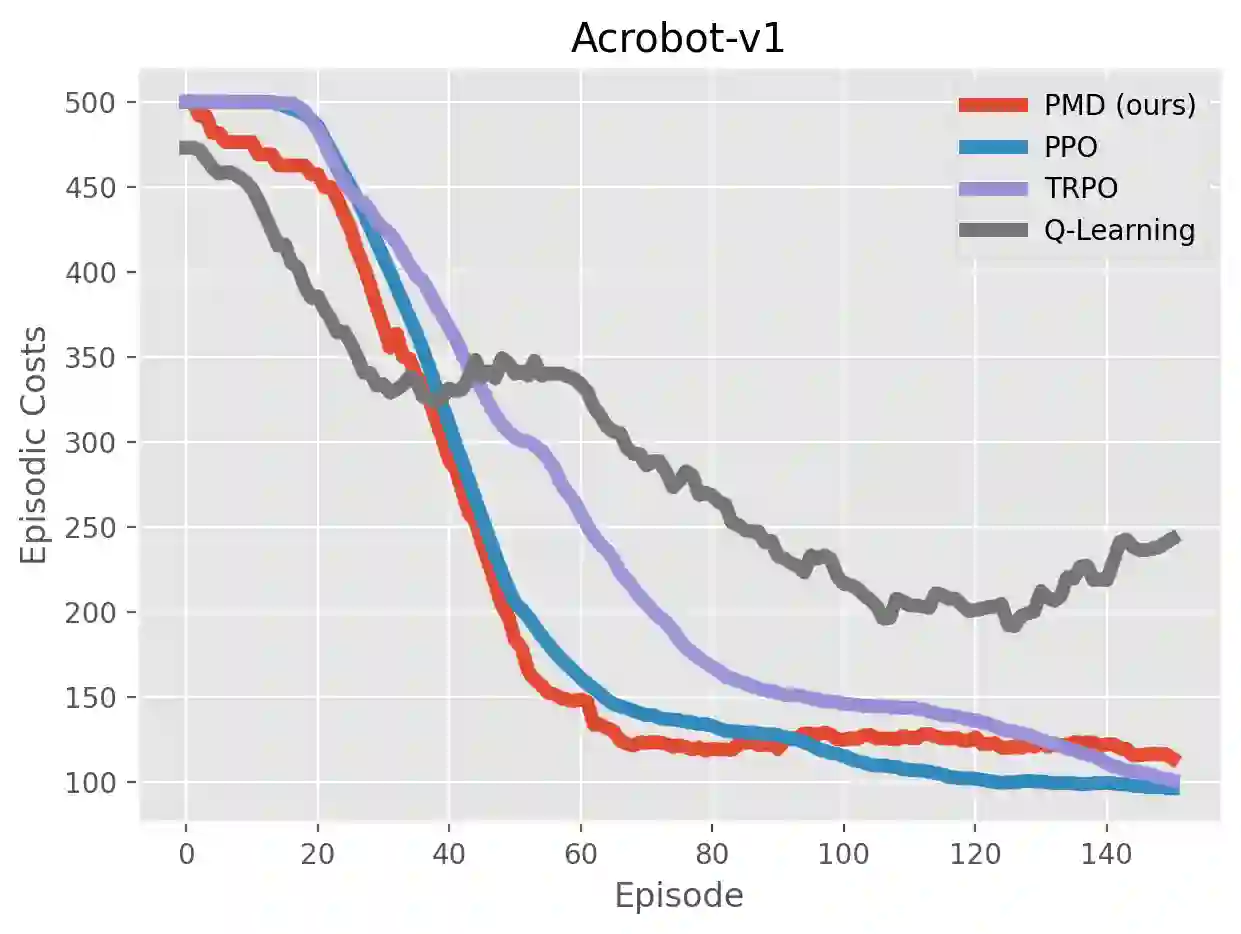
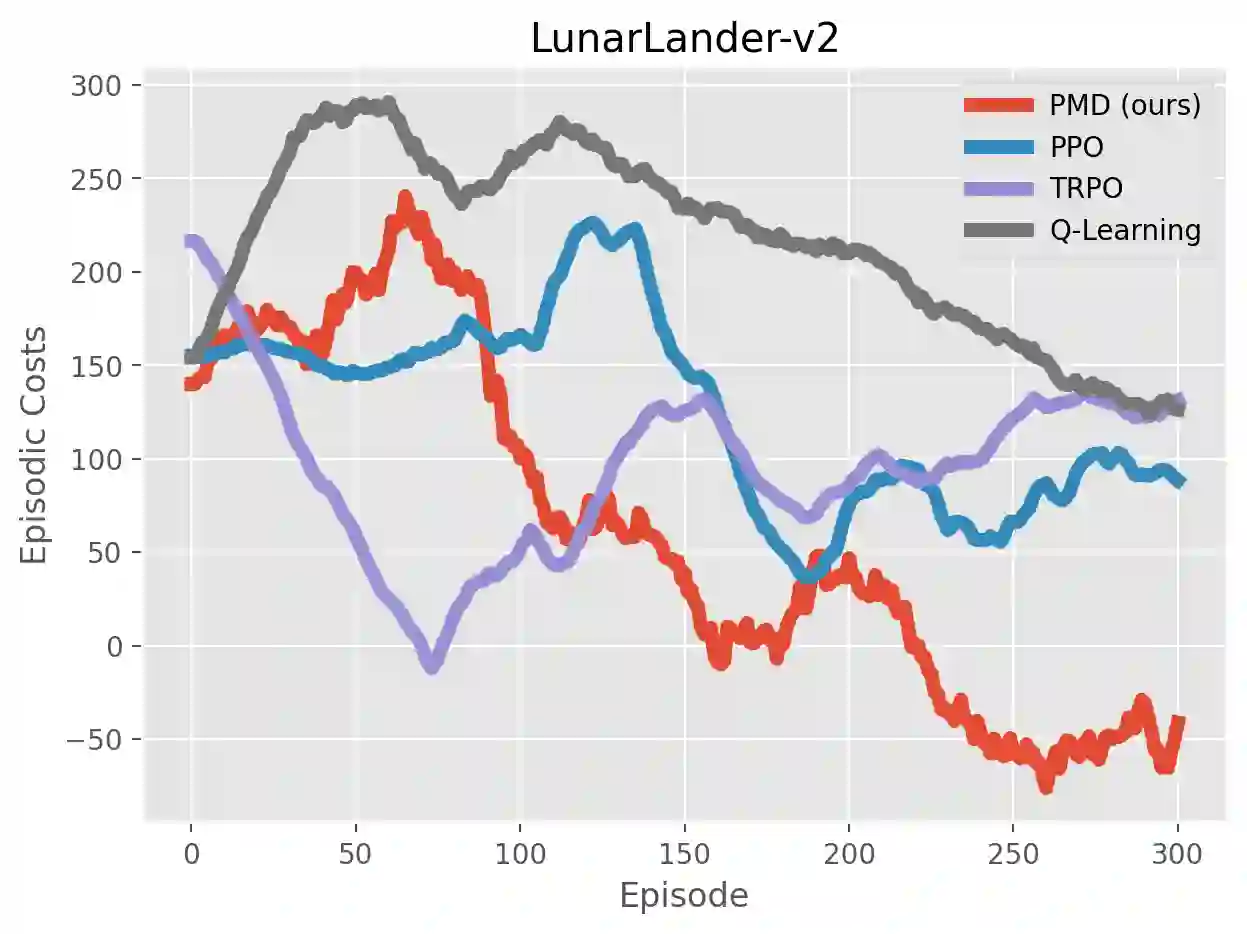
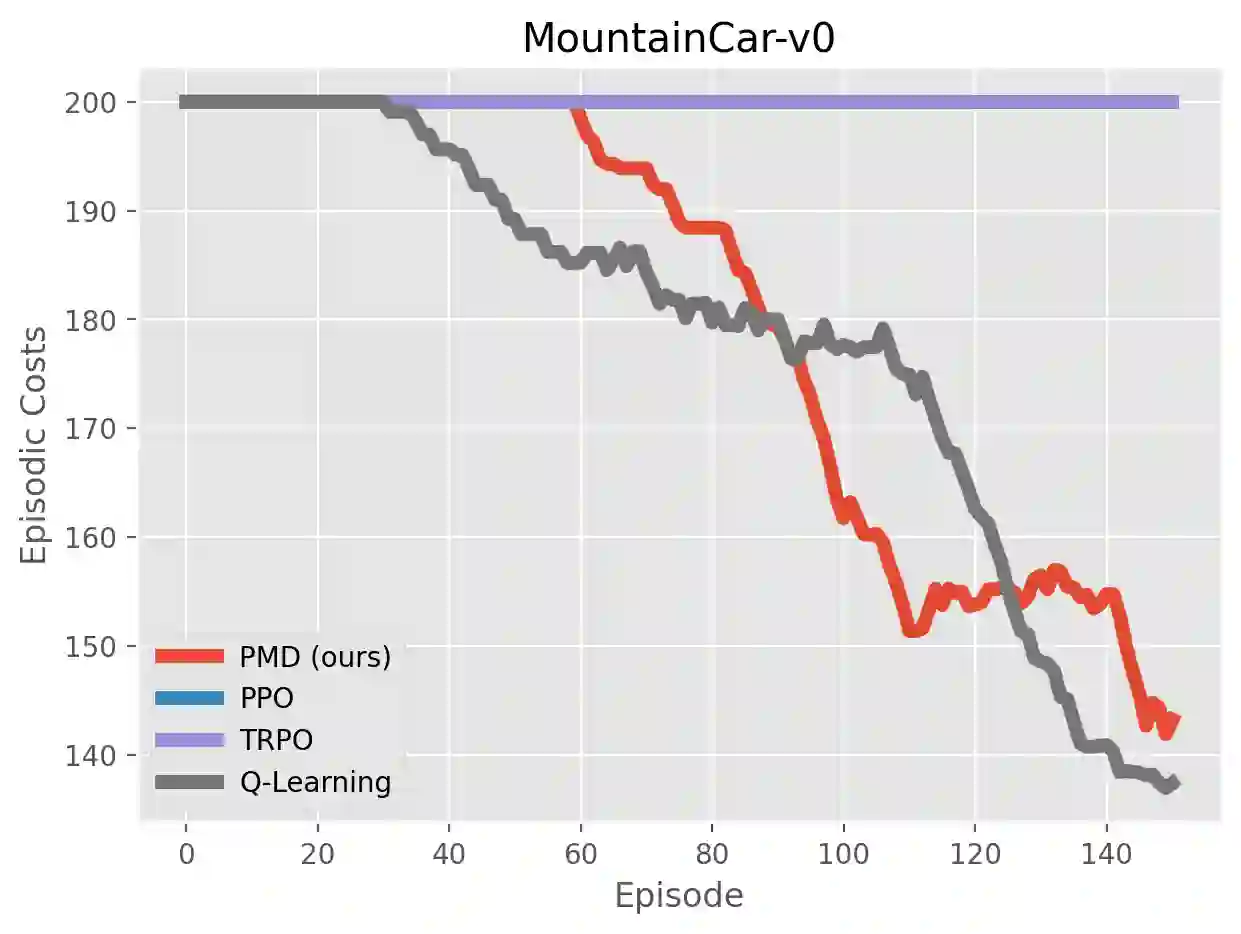
We study the problem of average-reward Markov decision processes (AMDPs) and develop novel first-order methods with strong theoretical guarantees for both policy evaluation and optimization. Existing on-policy evaluation methods suffer from sub-optimal convergence rates as well as failure in handling insufficiently random policies, e.g., deterministic policies, for lack of exploration. To remedy these issues, we develop a novel variance-reduced temporal difference (VRTD) method with linear function approximation for randomized policies along with optimal convergence guarantees, and an exploratory variance-reduced temporal difference (EVRTD) method for insufficiently random policies with comparable convergence guarantees. We further establish linear convergence rate on the bias of policy evaluation, which is essential for improving the overall sample complexity of policy optimization. On the other hand, compared with intensive research interest in finite sample analysis of policy gradient methods for discounted MDPs, existing studies on policy gradient methods for AMDPs mostly focus on regret bounds under restrictive assumptions on the underlying Markov processes (see, e.g., Abbasi-Yadkori et al., 2019), and they often lack guarantees on the overall sample complexities. Towards this end, we develop an average-reward variant of the stochastic policy mirror descent (SPMD) (Lan, 2022). We establish the first $\widetilde{\mathcal{O}}(\epsilon^{-2})$ sample complexity for solving AMDPs with policy gradient method under both the generative model (with unichain assumption) and Markovian noise model (with ergodic assumption). This bound can be further improved to $\widetilde{\mathcal{O}}(\epsilon^{-1})$ for solving regularized AMDPs. Our theoretical advantages are corroborated by numerical experiments.
翻译:我们研究平均回报的Markov 决策程序(AMDPs)问题,并开发具有政策评估和优化两方面强大理论保障的新一阶方法。现有的政策评价方法存在亚最佳趋同率,以及因缺乏探索而未能处理不完全随机政策(例如确定性政策)的问题。为了纠正这些问题,我们开发了一种新的差异减少时间差异(VRTD)方法,该方法以随机化政策为直线函数近似值,同时提供最佳趋同保证,以及探索性差异减少时间差异(EVRTD)方法,该方法以不完全随机的、具有类似趋同保证的政策。我们进一步建立了政策评价偏差的线性趋同率,这对于提高政策优化的总体抽样复杂性至关重要。另一方面,与研究对贴现 MDP 政策梯度方法的有限抽样分析的兴趣相比,目前对AMDPs 政策梯度方法的研究,主要侧重于根据对基本Markov 进程(例如Absi-Yadkori ) 模型进行遗憾度假设(见Absi-Yadkori et al) 方法,2019,该方法往往没有保证整个O 的内程政策变数。