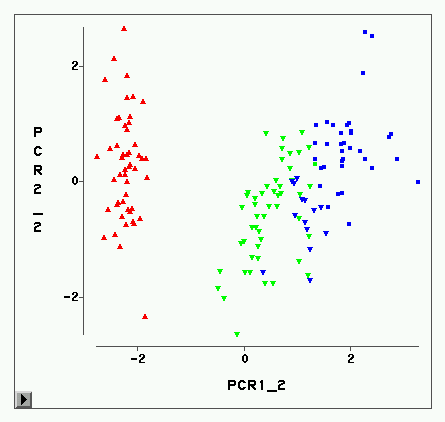
Modern wind turbines gather a wealth of data with Supervisory Control And Data Acquisition (SCADA) systems. We study the short-term mutual dependencies of a variety of observables by evaluating Pearson correlation matrices on a moving time window. Using clustering on these matrices, we identify multiple stable operational states, which characterize the non-stationarity of mutual dependencies at a single turbine. They represent different turbine operational settings. Moreover, we combine the clustering analysis with a construction of a stochastic process to study the switching dynamics of those states in more detail. Calculating the distances between correlation matrices we obtain a time series that describes the behavior of the complex system in a collective way. Assuming this time series to be governed by a Langevin equation, we estimate the deterministic (drift) and stochastic (diffusion) components of the dynamics to understand the underlying non-stationarity. After adapting our method to specific features of our data, we are able to study the dynamics of operational states and their transitions as well as to resolve hysteresis effects.
翻译:暂无翻译