Quantum Merkle Trees

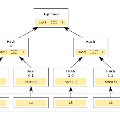
Commitment scheme is a central task in cryptography, where a party (typically called a prover) stores a piece of information (e.g., a bit string) with the promise of not changing it. This information can be accessed by another party (typically called the verifier), who can later learn the information and verify that it was not meddled with. Merkle tree is a well-known construction for doing so in a succinct manner, in which the verfier can learn any part of the information by receiving a short proof from the honest prover. Despite its significance in classical cryptography, there was no quantum analog of the Merkle tree. A direct generalization using the Quantum Random Oracle Model (QROM) does not seem to be secure. In this work, we propose the quantum Merkle tree. It is based on what we call the Quantum Haar Random Oracle Model (QHROM). In QHROM, both the prover and the verifier have access to a Haar random quantum oracle G and its inverse. Using the quantum Merkle tree, we propose a succinct quantum argument for the Gap-k-Local-Hamiltonian problem. We prove it is secure against semi-honest provers in QHROM and conjecture its general security. Assuming the Quantum PCP conjecture is true, this succinct argument extends to all of QMA. This work raises a number of interesting open research problems.