Budgeted Steiner Networks: Three Terminals with Equal Path Weights

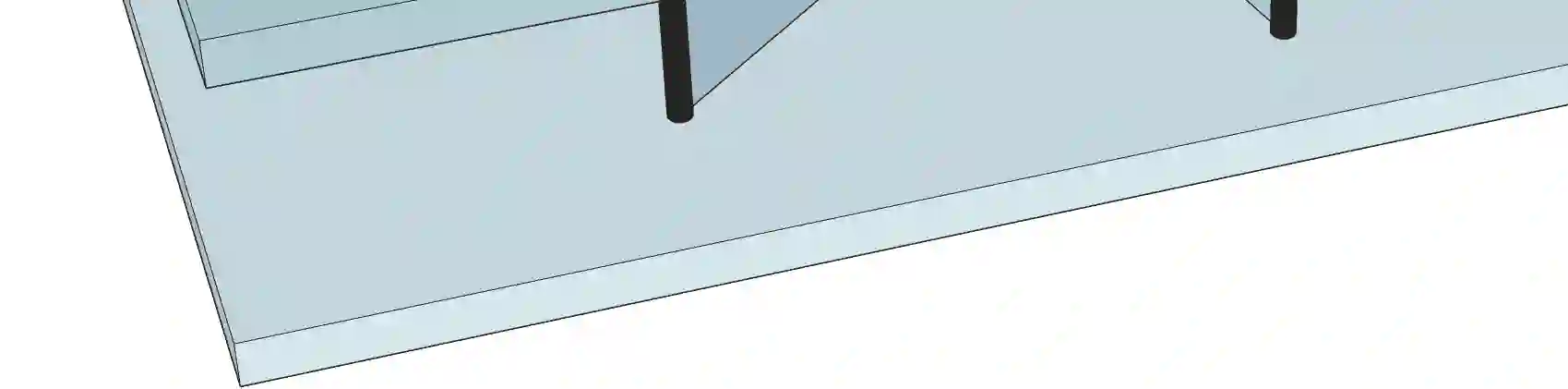
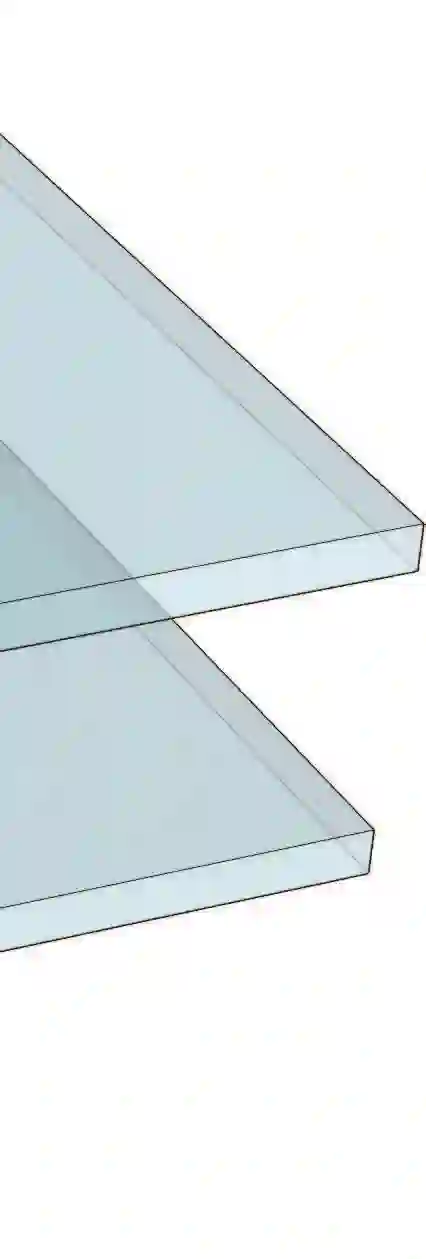
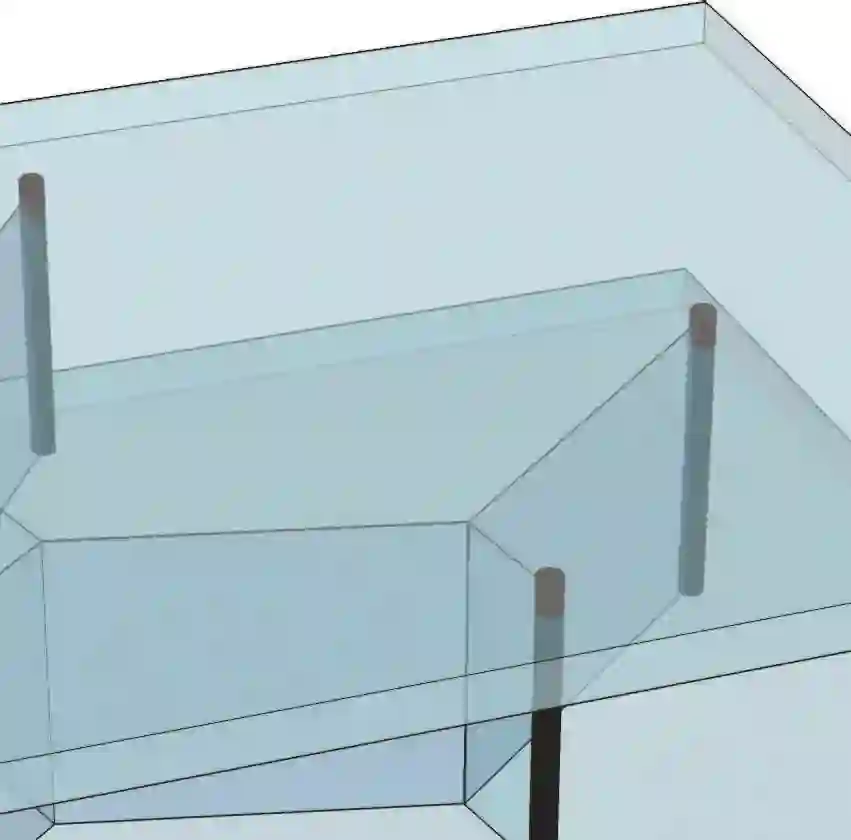
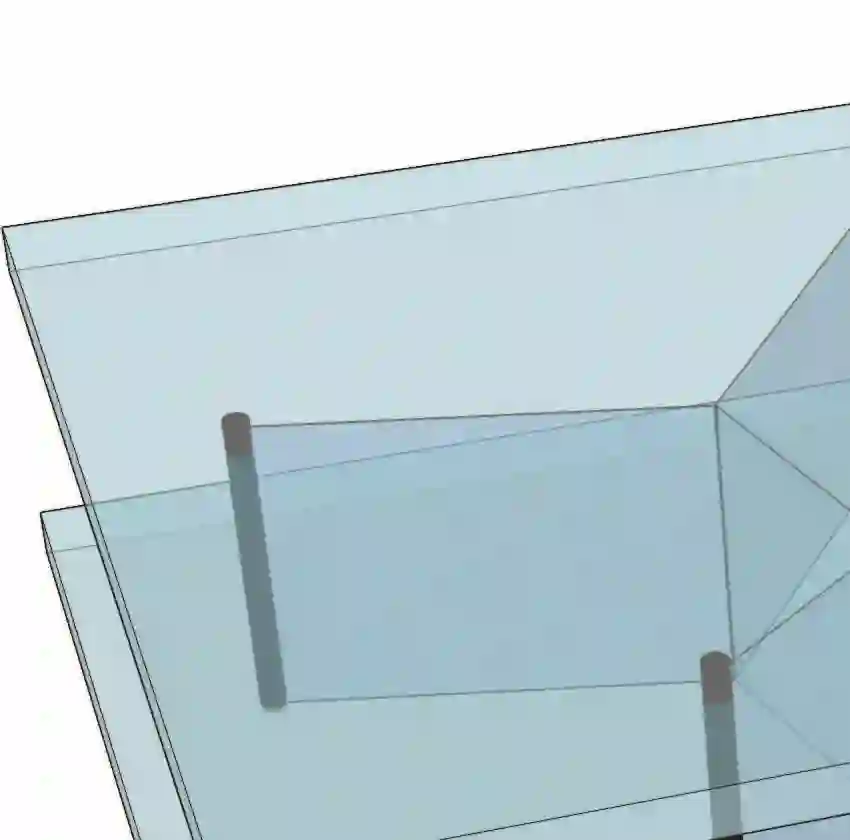
Given a set of terminals in 2D/3D, the network with the shortest total length that connects all terminals is a Steiner tree. On the other hand, with enough budget, every terminal can be connected to every other terminals via a straight edge, yielding a complete graph over all terminals. In this work, we study a generalization of Steiner trees asking what happens in between these two extremes. Focusing on three terminals with equal pairwise path weights, we characterize the full evolutionary pathway between the Steiner tree and the complete graph, which contains intriguing intermediate structures.