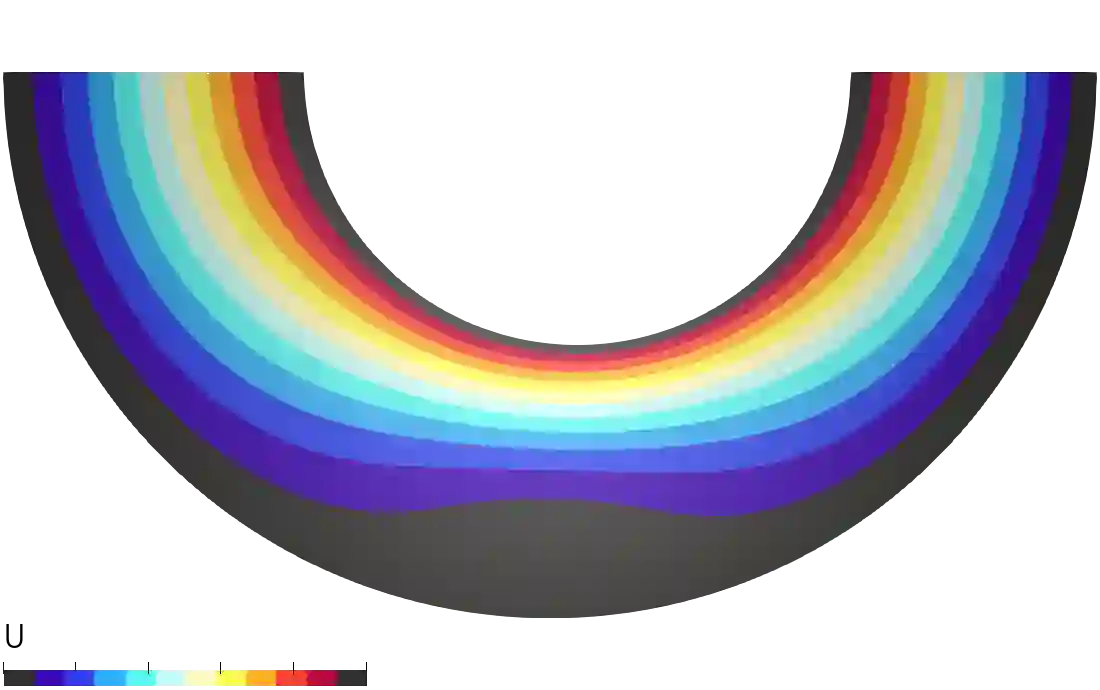
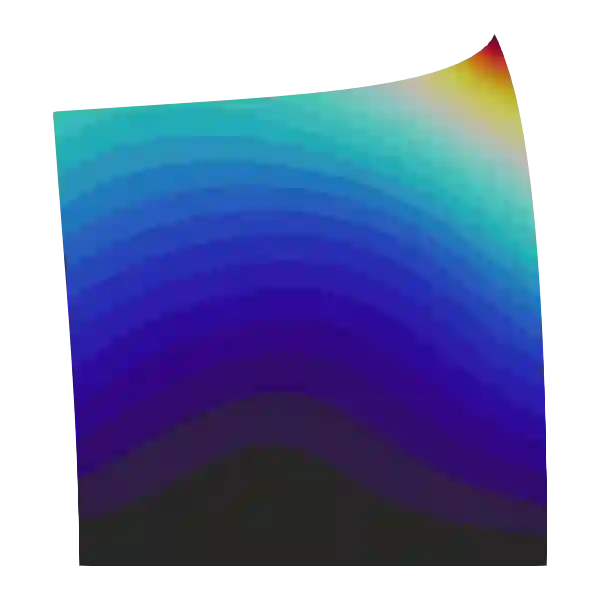
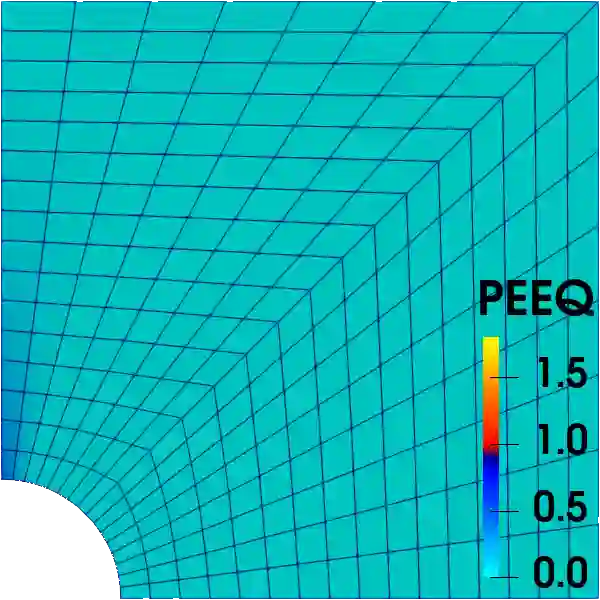
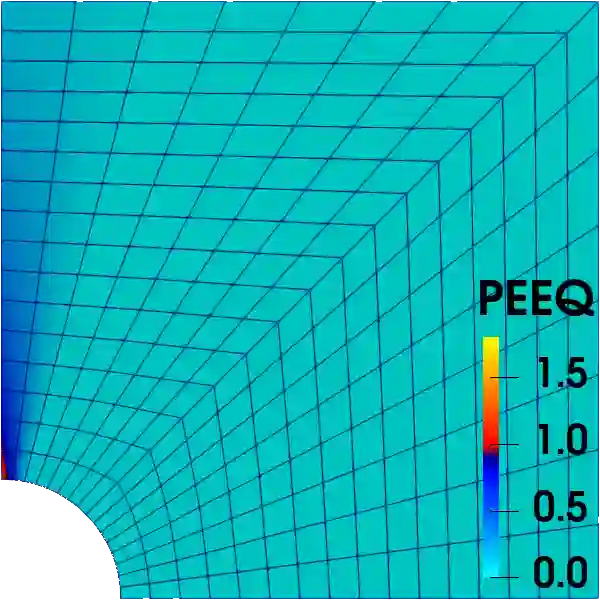
This work presents a general finite element formulation based on a six--field variational principle that incorporates the consistent couple stress theory. A simple, efficient and local iteration free solving procedure that covers both elastic and inelastic materials is derived to minimise computation cost. With proper interpolations, membrane elements of various nodes are proposed as the examples. The implemented finite elements are used to conduct numerical experiments to investigate the performance of the in-plane drilling degrees of freedom introduced by the consistent couple stress theory. The mesh dependency issue is also studied with both elastic and inelastic materials. It is shown that the consistent couple stress theory provides an objective definition of rotation compared with the Cauchy theory but additional regularisation (or other techniques) is required to overcome mesh/size dependency in softening or fracture related problems. In the case of hardening continuum problems and/or large characteristic lengths, the proposed formulation and elements offer a more reliable approach to model structures with both translational and rotational degrees of freedom.
翻译:这项工作提出了基于六领域差异原则的一般有限要素配方,其中纳入了一致的对口压力理论; 一种简单、高效和本地的无弹性迭代自由解答程序,既包括弹性材料,又包括弹性材料,以尽量减少计算成本; 通过适当的内插,提出各种节点的膜元素为例; 应用的有限元素用于进行数字实验,以调查由一致的对口压力理论引入的机内钻井自由度的性能; 也用弹性材料和无弹性材料研究网状依赖问题; 显示,一致的对口压力理论提供了与卡奥奇理论相比的轮换的客观定义,但需要额外的正规化(或其他技术)来克服软化或骨折相关问题中的网状/大小依赖性; 在硬化连续问题和/或大特征长度的情况下,拟议的构件和要素提供了一种更可靠的方法,用以模拟结构,既具有翻译自由度,又具有旋转自由度。