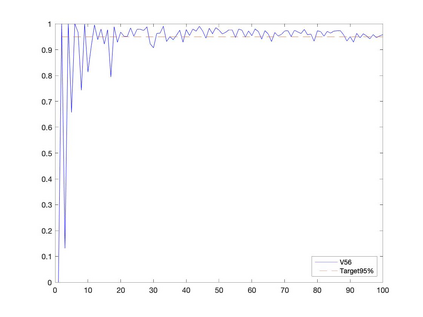
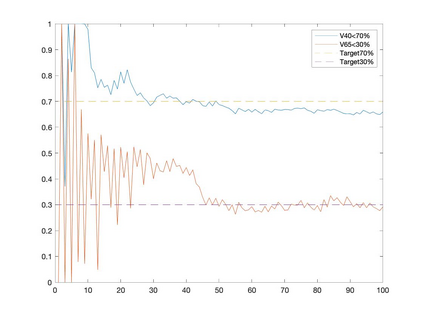
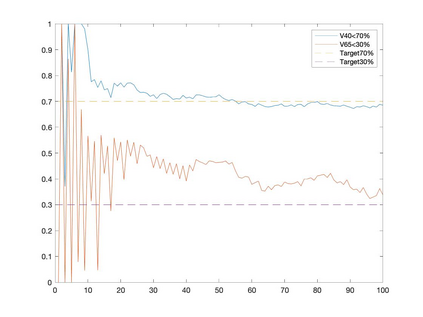
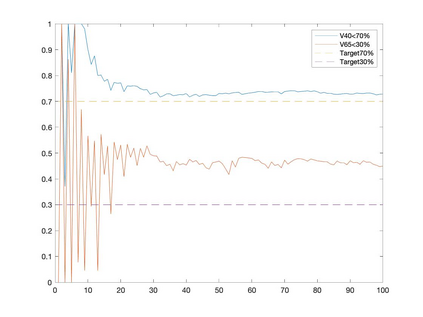
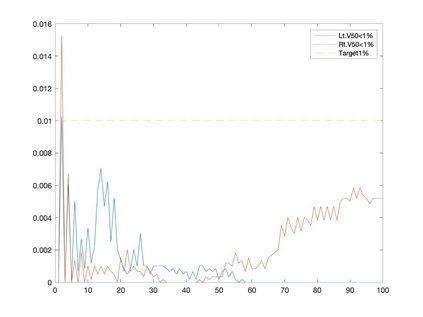
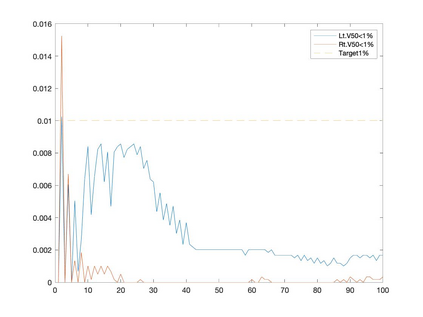
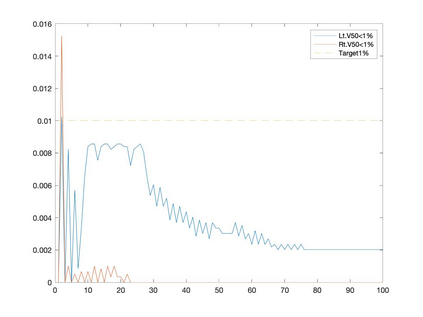
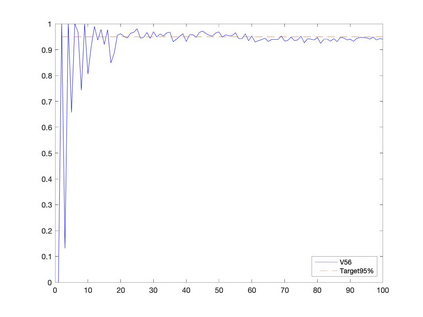
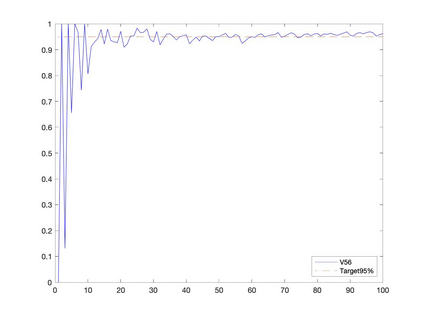
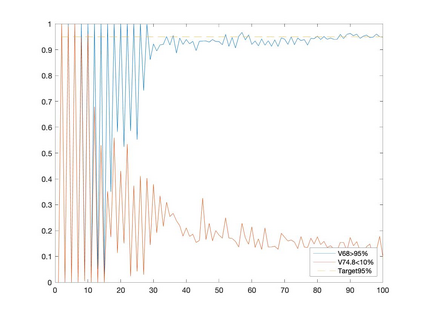
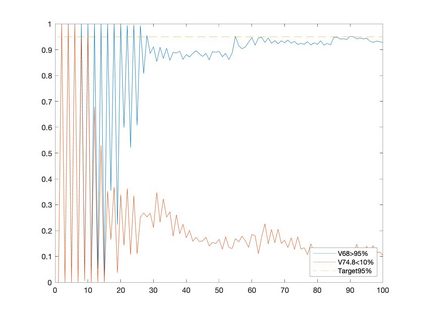
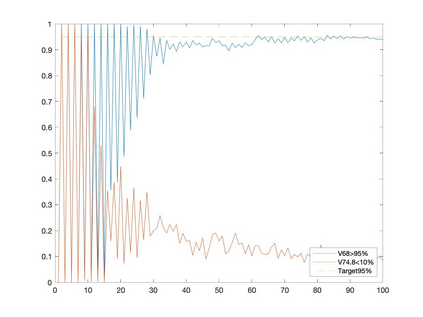
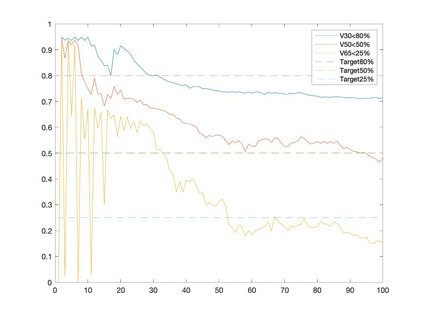
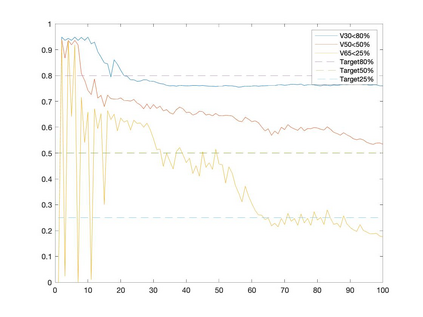
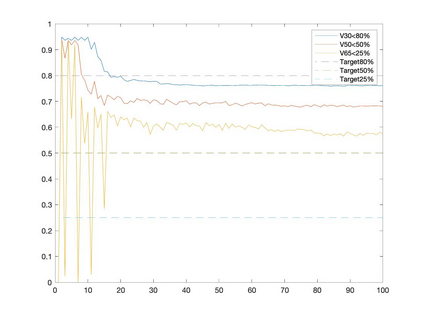
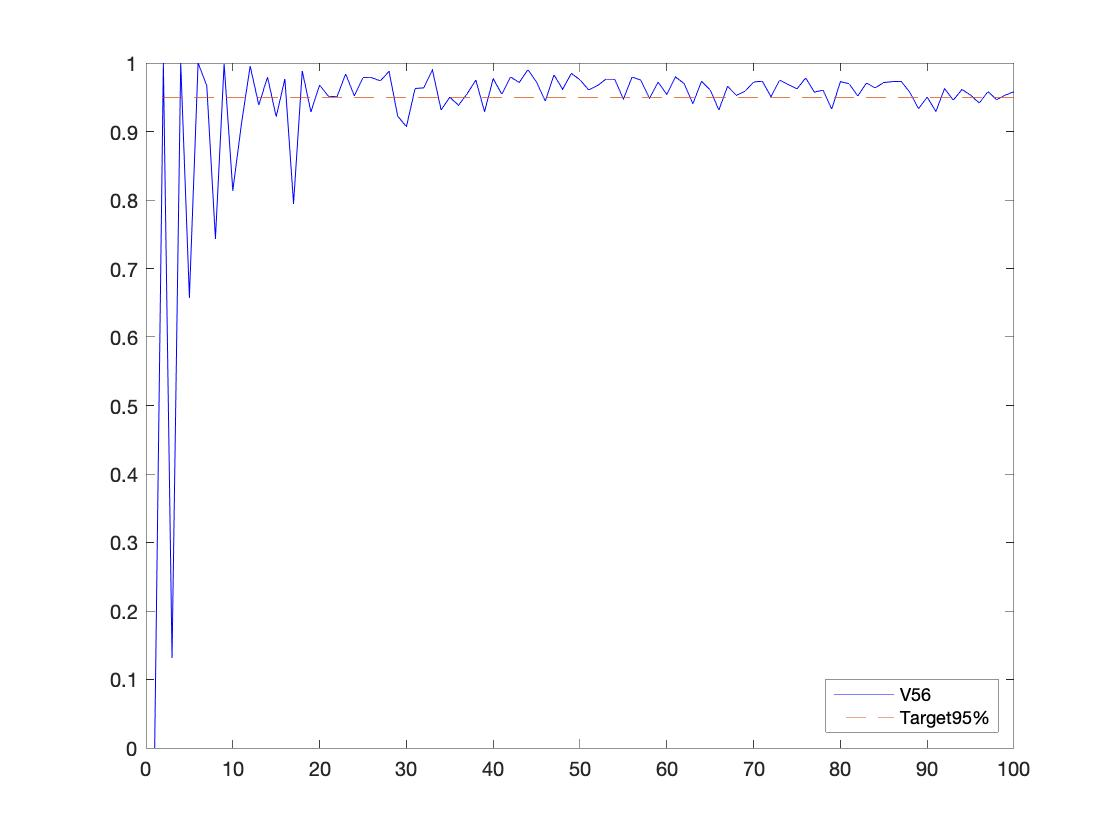
Conditional Gradient Methods for Convex Optimization with General Affine and Nonlinear Constraints

Conditional gradient methods have attracted much attention in both machine learning and optimization communities recently. These simple methods can guarantee the generation of sparse solutions. In addition, without the computation of full gradients, they can handle huge-scale problems sometimes even with an exponentially increasing number of decision variables. This paper aims to significantly expand the application areas of these methods by presenting new conditional gradient methods for solving convex optimization problems with general affine and nonlinear constraints. More specifically, we first present a new constraint extrapolated condition gradient (CoexCG) method that can achieve an ${\cal O}(1/\epsilon^2)$ iteration complexity for both smooth and structured nonsmooth function constrained convex optimization. We further develop novel variants of CoexCG, namely constraint extrapolated and dual regularized conditional gradient (CoexDurCG) methods, that can achieve similar iteration complexity to CoexCG but allow adaptive selection for algorithmic parameters. We illustrate the effectiveness of these methods for solving an important class of radiation therapy treatment planning problems arising from healthcare industry. To the best of our knowledge, all the algorithmic schemes and their complexity results are new in the area of projection-free methods.