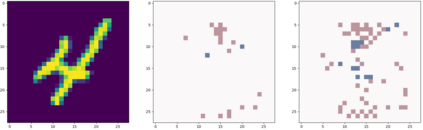
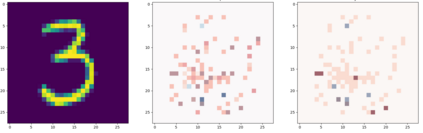
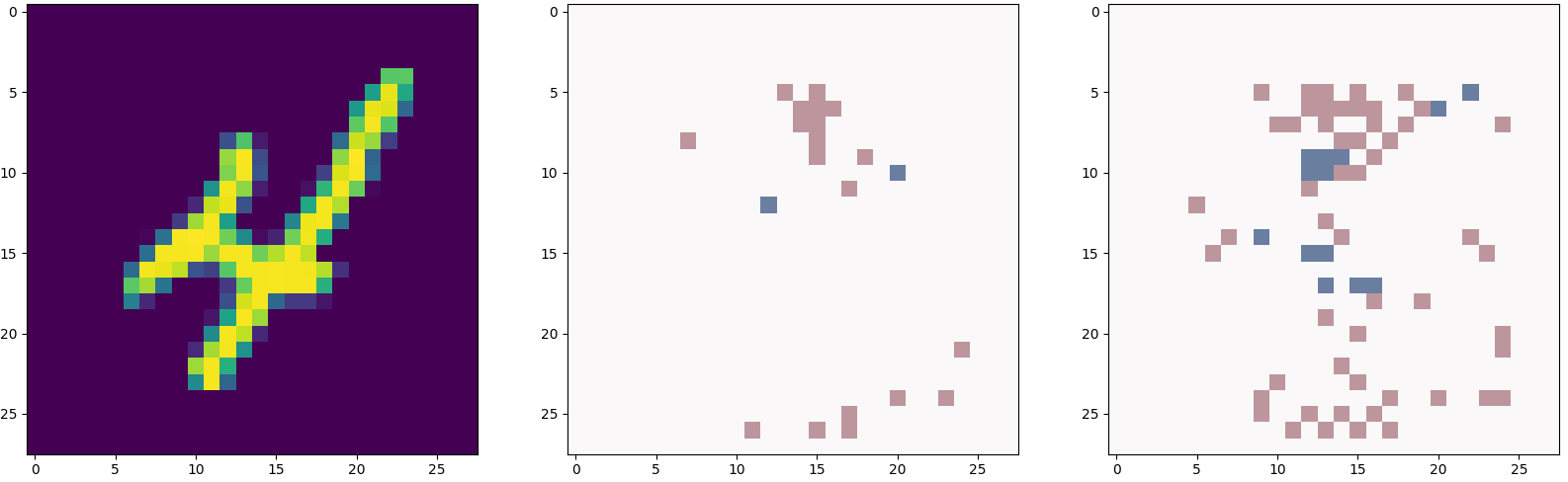
Decision trees have long been recognized as models of choice in sensitive applications where interpretability is of paramount importance. In this paper, we examine the computational ability of Boolean decision trees in deriving, minimizing, and counting sufficient reasons and contrastive explanations. We prove that the set of all sufficient reasons of minimal size for an instance given a decision tree can be exponentially larger than the size of the input (the instance and the decision tree). Therefore, generating the full set of sufficient reasons can be out of reach. In addition, computing a single sufficient reason does not prove enough in general; indeed, two sufficient reasons for the same instance may differ on many features. To deal with this issue and generate synthetic views of the set of all sufficient reasons, we introduce the notions of relevant features and of necessary features that characterize the (possibly negated) features appearing in at least one or in every sufficient reason, and we show that they can be computed in polynomial time. We also introduce the notion of explanatory importance, that indicates how frequent each (possibly negated) feature is in the set of all sufficient reasons. We show how the explanatory importance of a feature and the number of sufficient reasons can be obtained via a model counting operation, which turns out to be practical in many cases. We also explain how to enumerate sufficient reasons of minimal size. We finally show that, unlike sufficient reasons, the set of all contrastive explanations for an instance given a decision tree can be derived, minimized and counted in polynomial time.
翻译:在解释至关重要的敏感应用中,决策树长期以来被确认为选择模式。在本文件中,我们研究了布利恩决策树的计算能力,从中得出、尽量减少和计算充分的理由和对比性的解释。我们证明,对某一决策树而言,最小大小的所有充分理由可能比投入(实例和决策树)的大小大得多。因此,产生全部充分理由可能无法实现。此外,计算一个单一的充分理由一般不足以证明足够;事实上,同一理由的第二个充分理由在许多特点上可能有所不同。为了处理这一问题,并对所有充分理由集产生综合看法,我们引入了相关特点的概念和必要特点的概念,这些特点在至少一个或每一个充分理由中都有(可能否定的),我们证明这些特点可以比输入的大小大得多。我们还提出解释性概念的重要性,说明每个(可能否定的)单一充分理由在一系列充分的理由中都有多频繁。我们展示了一个特点的解释性重要性,并对所有充分理由的完整解释性解释性理由的精确性数字,我们最后用一个模型来解释一个充分的理由来解释。我们用多少解释。我们用一个最起码的理由解释性的理由来解释一个最起码的理由来解释。我们用最起码的理由来解释。我们用最起码的理由来解释。我们用最起码的理由来解释一个例子来解释一个最起码的理由来解释。