The Computation of Approximate Generalized Feedback Nash Equilibria

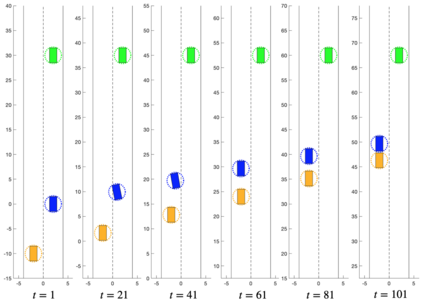
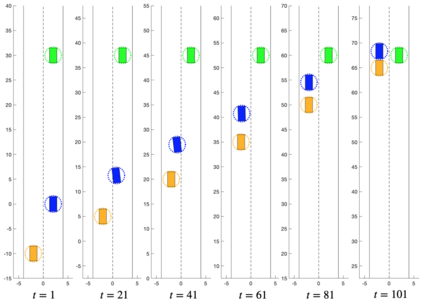
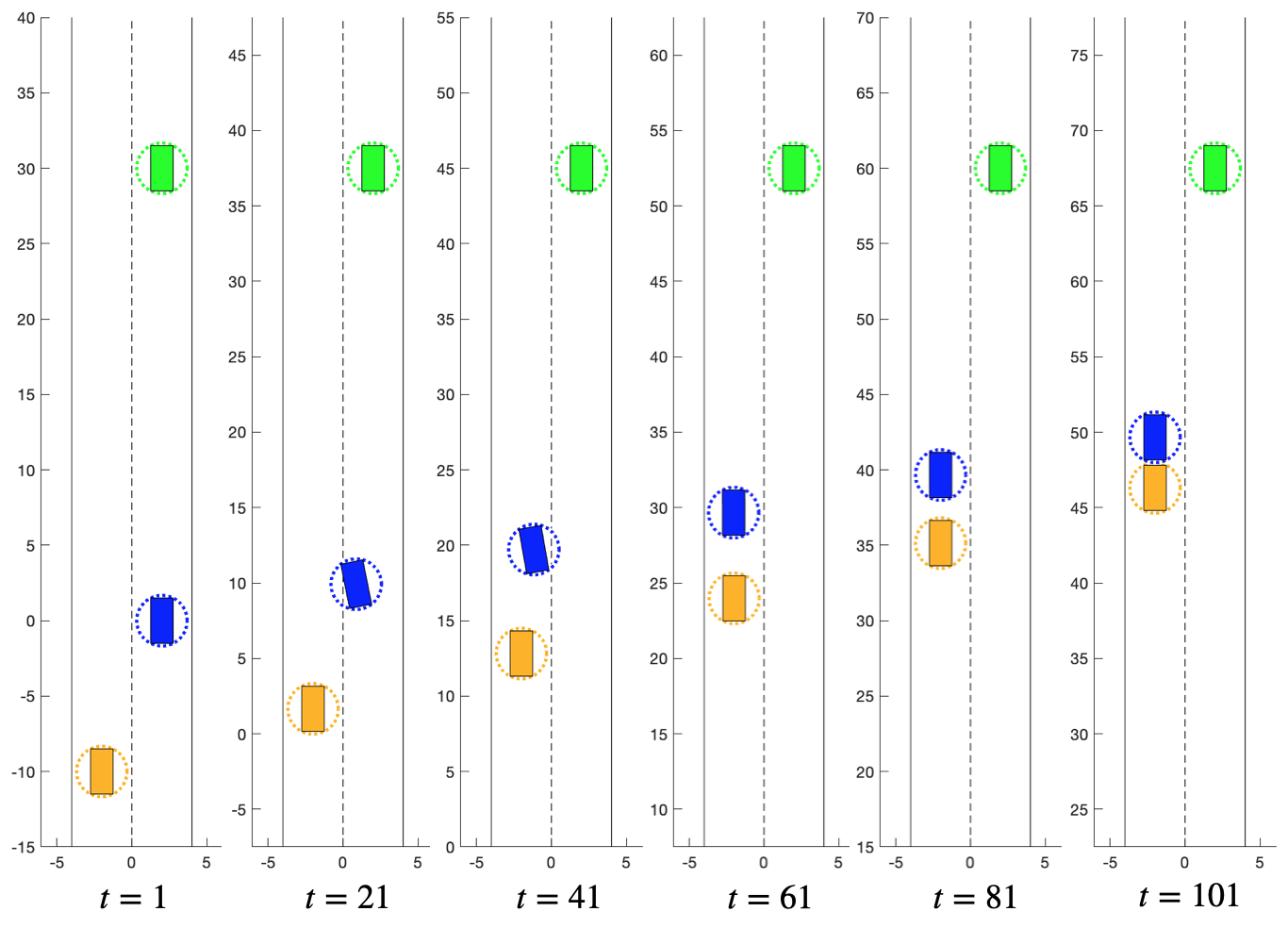
We present the concept of a Generalized Feedback Nash Equilibrium (GFNE) in dynamic games, extending the Feedback Nash Equilibrium concept to games in which players are subject to state and input constraints. We formalize necessary and sufficient conditions for (local) GFNE solutions at the trajectory level, which enable the development of efficient numerical methods for their computation. Specifically, we propose a Newton-style method for finding game trajectories which satisfy the necessary conditions, which can then be checked against the sufficiency conditions. We show that the evaluation of the necessary conditions in general requires computing a series of nested, implicitly-defined derivatives, which quickly becomes intractable. To this end, we introduce an approximation to the necessary conditions which is amenable to efficient evaluation, and in turn, computation of solutions. We term the solutions to the approximate necessary conditions Generalized Feedback Quasi Nash Equilibria (GFQNE), and we introduce numerical methods for their computation. In particular, we develop a Sequential Linear-Quadratic Game approach, in which a locally approximate LQ game is solved at each iteration. The development of this method relies on the ability to compute a GFNE to inequality- and equality-constrained LQ games, and therefore specific methods for the solution of these special cases are developed in detail. We demonstrate the effectiveness of the proposed solution approach on a dynamic game arising in an autonomous driving application.