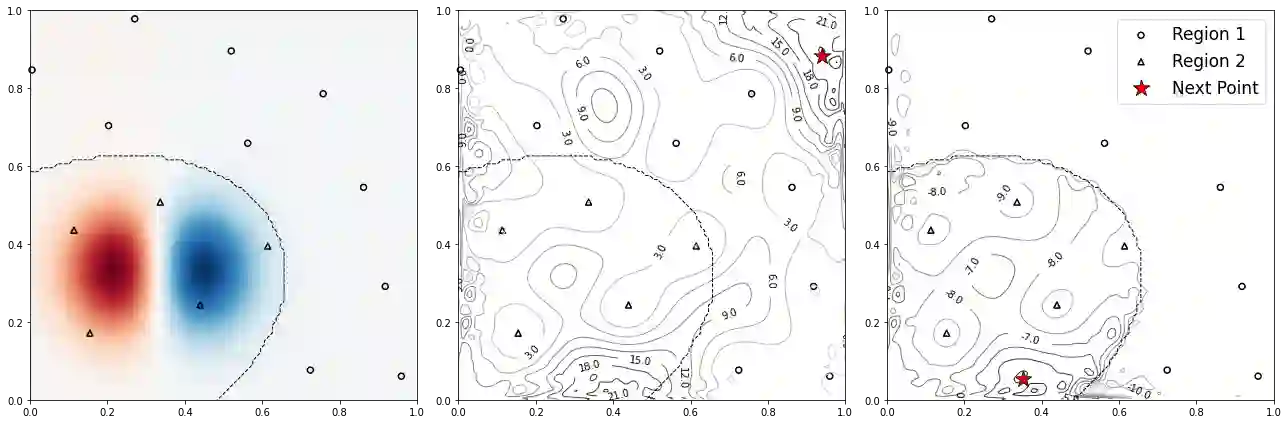
Active learning is a subfield of machine learning that focuses on improving the data collection efficiency of expensive-to-evaluate systems. Especially, active learning integrated surrogate modeling has shown remarkable performance in computationally demanding engineering systems. However, the existence of heterogeneity in underlying systems may adversely affect the performance of active learning. In order to improve the learning efficiency under this regime, we propose the partitioned active learning that seeks the most informative design points for partitioned Gaussian process modeling of heterogeneous systems. The proposed active learning consists of two systematic subsequent steps: the global searching scheme accelerates the exploration of active learning by investigating the most uncertain design space, and the local searching exploits the circumscribed information induced by the local GP. We also propose Cholesky update driven numerical remedies for our active learning to address the computational complexity challenge. The proposed method is applied to numerical simulations and two real-world case studies about (i) the cost-efficient automatic fuselage shape control in aerospace manufacturing; and (ii) the optimal design of tribocorrosion-resistant alloys in materials science. The results show that our approach outperforms benchmark methods with respect to prediction accuracy and computational efficiency.
翻译:积极的学习是机械学习的一个子领域,重点是提高昂贵到评估系统的数据收集效率。特别是,积极的学习综合替代模型在计算要求很高的工程系统中表现出了显著的性能。然而,基础系统中的异质性可能会对积极学习的绩效产生不利影响。为了提高这个制度下的学习效率,我们提议了分解的积极学习,以寻求为分散的多元系统高萨进程建模提供最丰富的设计点。拟议的积极学习包括两个系统化的后续步骤:全球搜索计划通过调查最不确定的设计空间加快积极学习的探索,而当地搜索则利用当地GP提供的受限制的信息。我们还提议Choolesky更新驱动的数字补救措施,以积极学习解决计算复杂性的挑战。拟议的方法应用于数字模拟和两个真实世界案例研究:(一) 航空航天制造中成本效率高的自动机能形状控制;以及(二) 最佳地设计材料科学中抗三波质压合金合金。结果显示,我们的方法超过了预测的精确度和精确度基准计算方法。