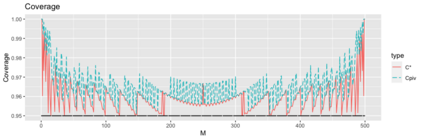
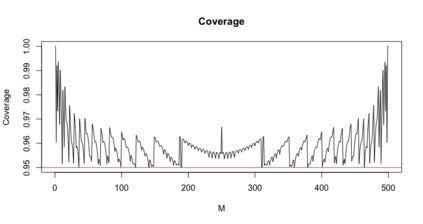
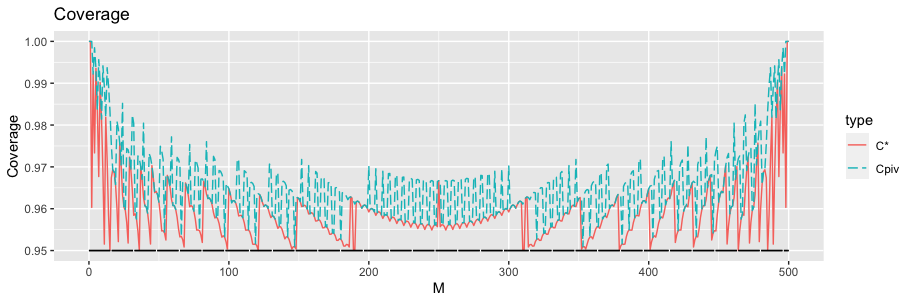
We present an efficient method of calculating exact confidence intervals for the hypergeometric parameter representing the number of "successes," or "special items," in the population. The method inverts minimum-width acceptance intervals after shifting them to make their endpoints nondecreasing while preserving their level. The resulting set of confidence intervals achieves minimum possible average size, and even in comparison with confidence sets not required to be intervals it attains the minimum possible cardinality most of the time, and always within $1$. The method compares favorably with existing methods not only in the size of the intervals but also in the time required to compute them. The available \textsf{R} package \texttt{hyperMCI} implements the proposed method.
翻译:我们提出了一个有效的方法,用于计算超地球测量参数的精确信任度间隔, 代表人口“ 成功” 或“ 特殊项目” 的数量。 这种方法在移动端点使其在保持其水平的同时不降低其端点之后, 将最小接受度间隔倒转。 由此形成的一套信任度间隔达到了可能的最低平均尺寸, 即便与信任度间隔相比, 也不必有间隔, 以达到最起码的可能基点, 并且总是在$$之内。 该方法不仅在间隔的大小上, 而且在计算它们所需的时间上, 也比现有的方法要好。 可用的 \ textsf{R} 包\ textt{hyperMCI} 执行拟议的方法 。