A virtual element method for the elasticity spectral problem allowing small edges

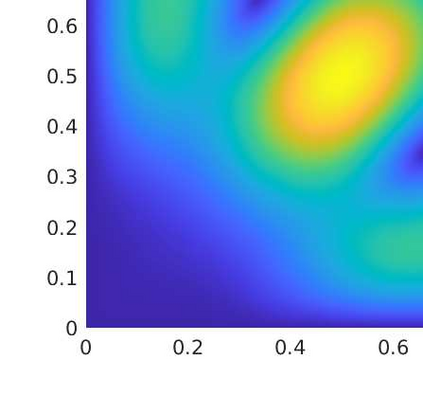
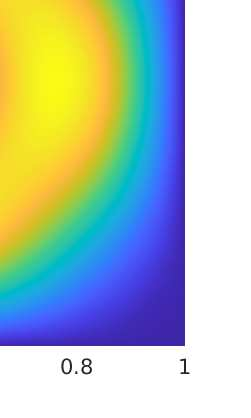
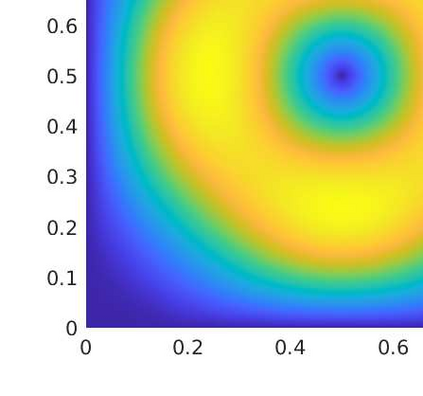
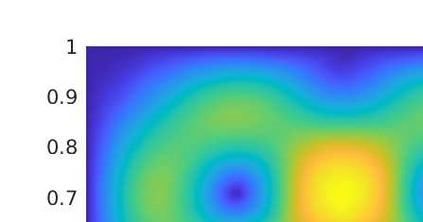
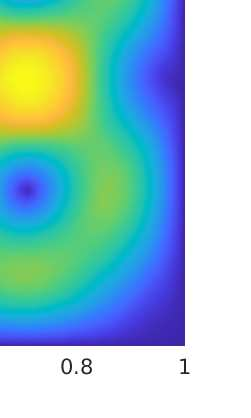
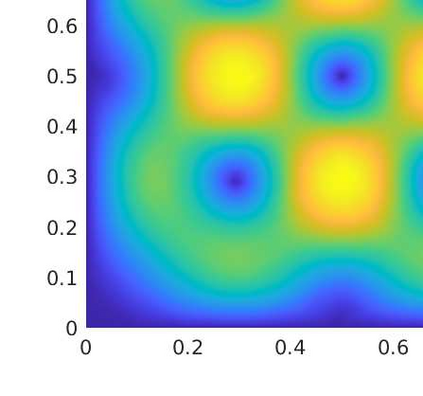
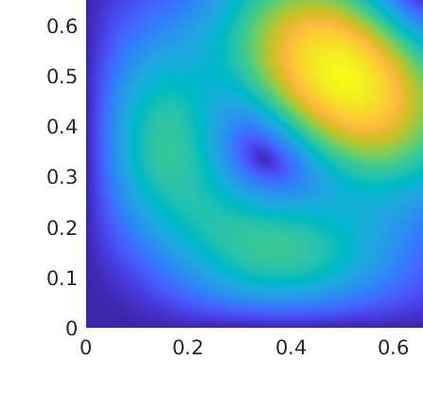
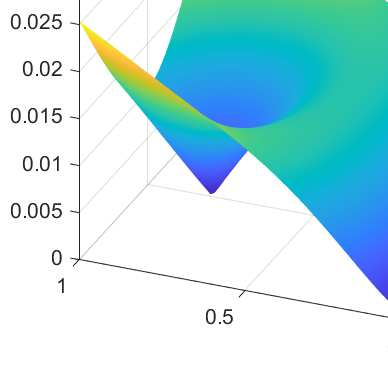
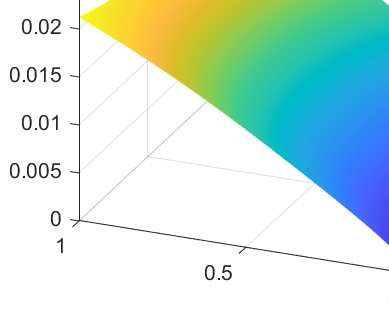
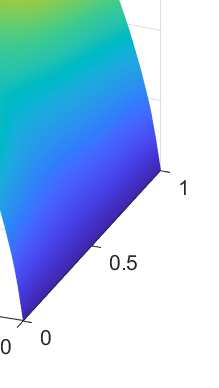
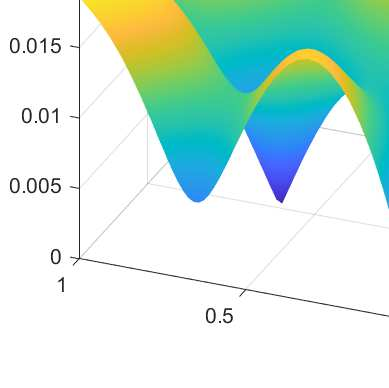
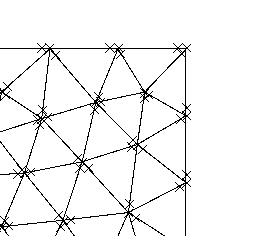
In this paper we analyze a virtual element method for the two dimensional elasticity spectral problem allowing small edges. Under this approach, and with the aid of the theory of compact operators, we prove convergence of the proposed VEM and error estimates, where the influence of the Lam\'e constants is presented. We present a series of numerical tests to assess the performance of the method where we analyze the effects of the Poisson ratio on the computation of the order of convergence, together with the effects of the stabilization term on the arising of spurious eigenvalues.