Weak Collocation Regression method: fast reveal hidden stochastic dynamics from high-dimensional aggregate data

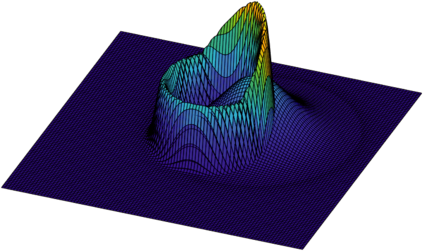
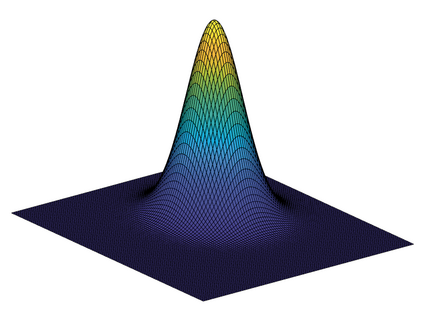
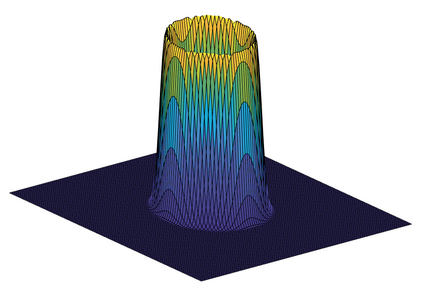
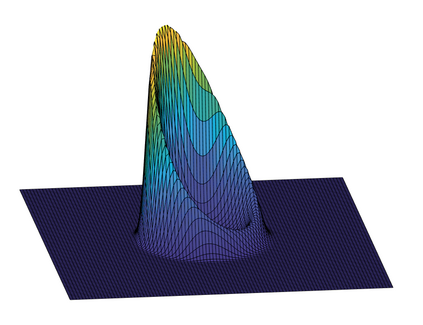
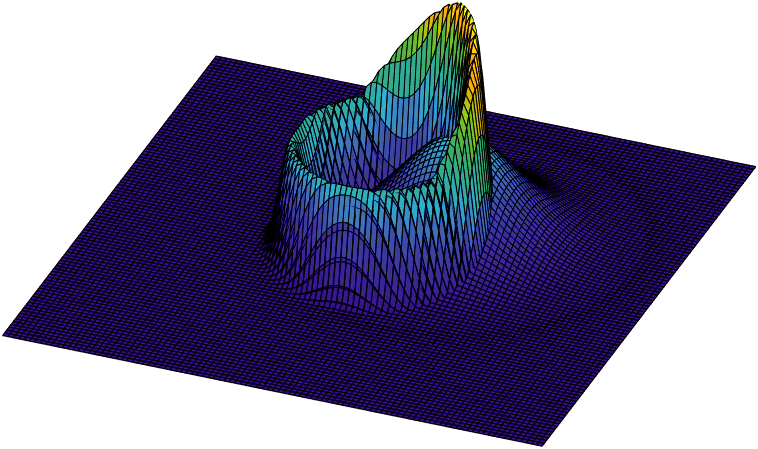
Revealing hidden dynamics from the stochastic data is a challenging problem as randomness takes part in the evolution of the data. The problem becomes exceedingly complex when the trajectories of the stochastic data are absent in many scenarios. Here we present an approach to effectively modeling the dynamics of the stochastic data without trajectories based on the weak form of the Fokker-Planck (FP) equation, which governs the evolution of the density function in the Brownian process. Taking the collocations of Gaussian functions as the test functions in the weak form of the FP equation, we transfer the derivatives to the Gaussian functions and thus approximate the weak form by the expectational sum of the data. With a dictionary representation of the unknown terms, a linear system is built and then solved by the regression, revealing the unknown dynamics of the data. Hence, we name the method with the Weak Collocation Regression (WCK) method for its three key components: weak form, collocation of Gaussian kernels, and regression. The numerical experiments show that our method is flexible and fast, which reveals the dynamics within seconds in multi-dimensional problems and can be easily extended to high-dimensional data such as 20 dimensions. WCR can also correctly identify the hidden dynamics of the complex tasks with variable-dependent diffusion and coupled drift, and the performance is robust, achieving high accuracy in the case with noise added.