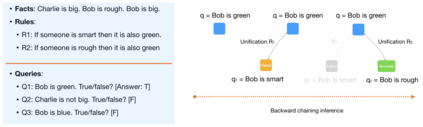
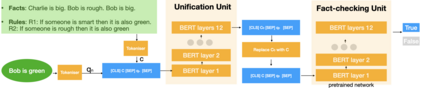
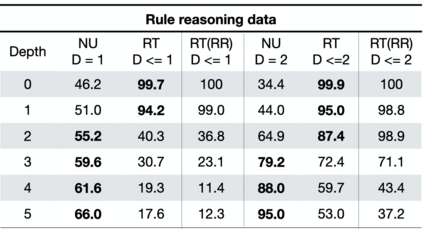
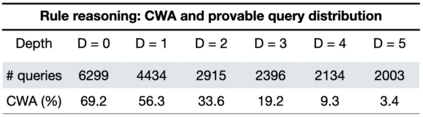
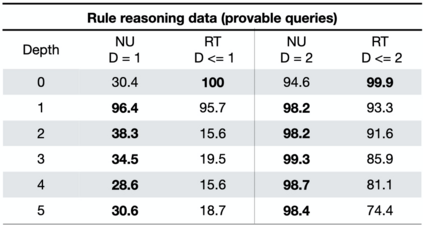
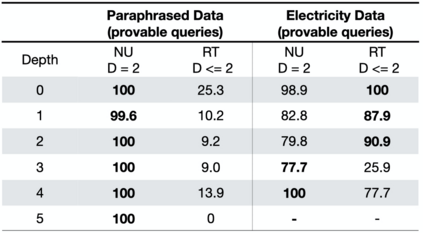
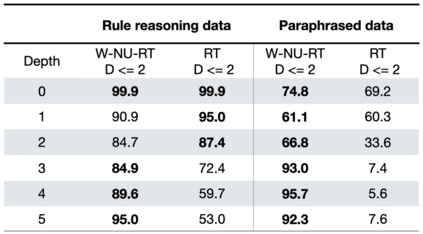
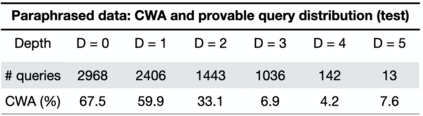
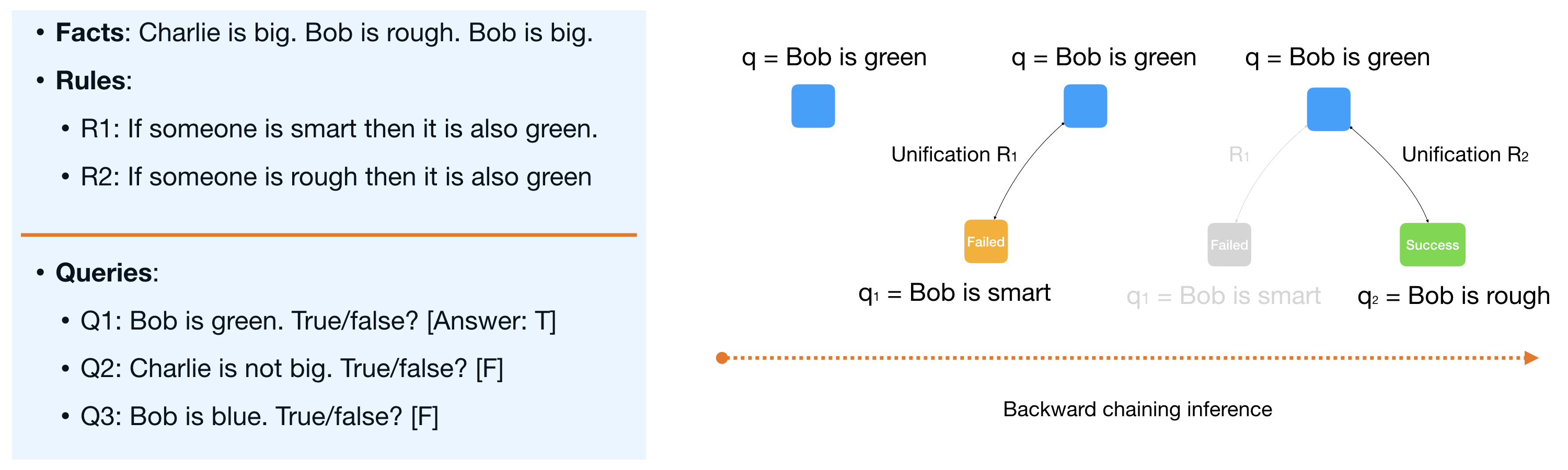
Automated Theorem Proving (ATP) deals with the development of computer programs being able to show that some conjectures (queries) are a logical consequence of a set of axioms (facts and rules). There exists several successful ATPs where conjectures and axioms are formally provided (e.g. formalised as First Order Logic formulas). Recent approaches, such as (Clark et al., 2020), have proposed transformer-based architectures for deriving conjectures given axioms expressed in natural language (English). The conjecture is verified through a binary text classifier, where the transformers model is trained to predict the truth value of a conjecture given the axioms. The RuleTaker approach of (Clark et al., 2020) achieves appealing results both in terms of accuracy and in the ability to generalize, showing that when the model is trained with deep enough queries (at least 3 inference steps), the transformers are able to correctly answer the majority of queries (97.6%) that require up to 5 inference steps. In this work we propose a new architecture, namely the Neural Unifier, and a relative training procedure, which achieves state-of-the-art results in term of generalisation, showing that mimicking a well-known inference procedure, the backward chaining, it is possible to answer deep queries even when the model is trained only on shallow ones. The approach is demonstrated in experiments using a diverse set of benchmark data.
翻译:自动Theorem 验证( ATP) 涉及计算机程序开发的计算机程序, 能够显示某些猜想( 查询) 是一组正数( 事实和规则) 的逻辑结果。 存在一些成功的 ATP, 正式提供猜想和正数( 例如, 正规化为第一级逻辑公式 ) 。 最新的方法, 如( Clark et al., 2020), 提出了基于变动器的架构, 以得出以自然语言( 英文) 表达的正数表达的共数变量的猜想( 质数) 。 猜想通过一个双数文本分类法( 质数) 校验, 使变异模型能够预测一个正数的真数值 。 变异数模型( Clark et al., 2020) 方法在准确性和概括化能力两方面都具有吸引力, 表明当模型经过深度查询( 至少3个深度步骤 ) 时, 变换者能够正确回答大多数新的查询( 97. 6%), 需要经过训练的正数的正数的正数的轨方法, 显示一个直数的轨方法, 显示一般的直数程序。 在显示一般的校正数中, 在显示的校准中, 的校准中, 的校准中, 显示一个直数程序是显示的轨中, 直数程序。