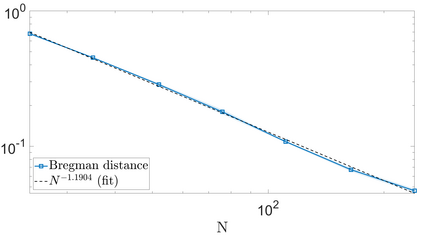
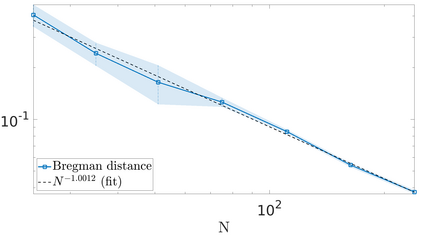
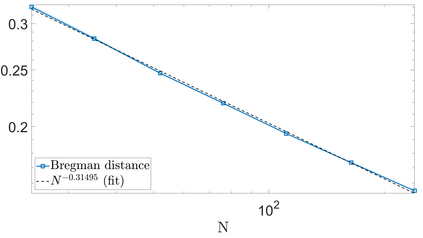
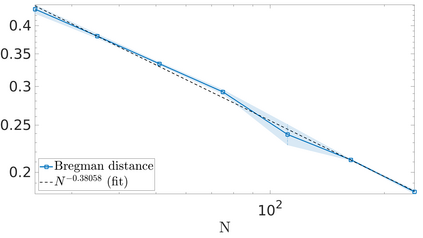
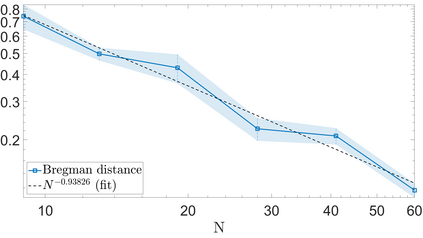
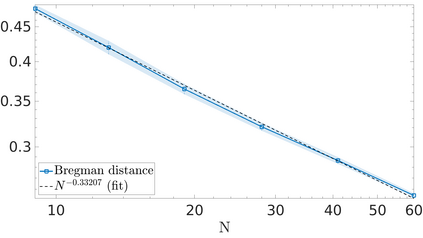
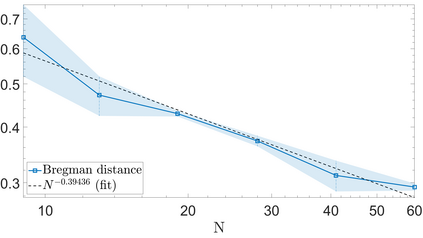
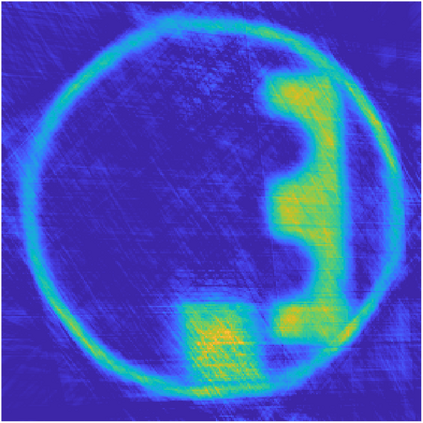
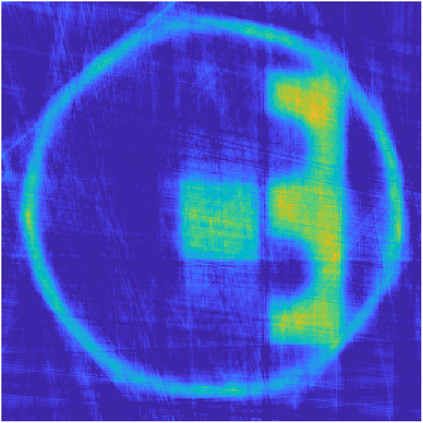
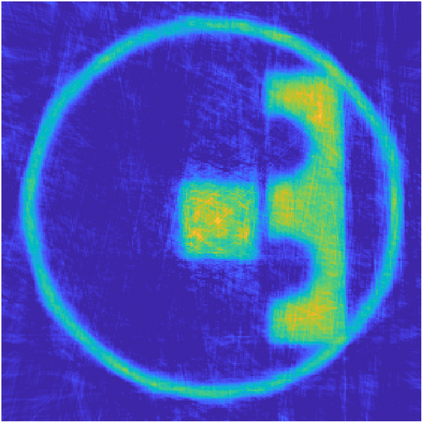
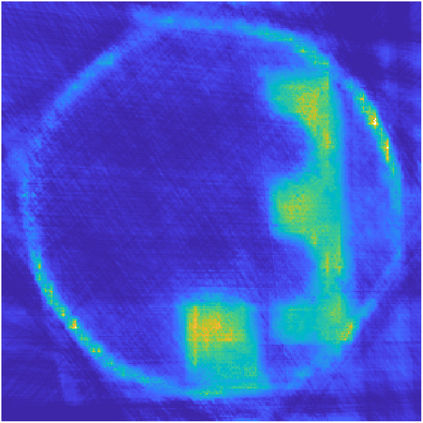
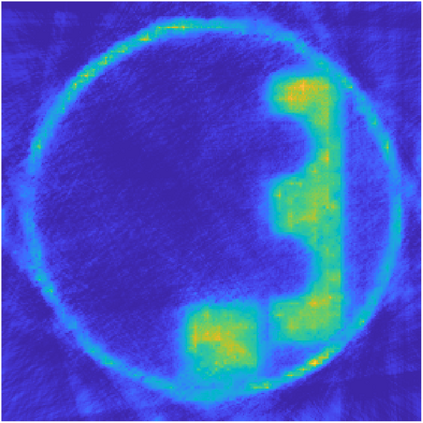
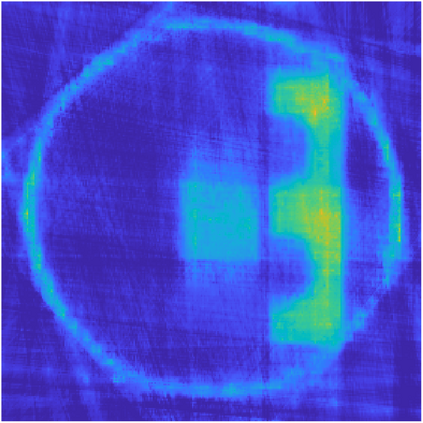
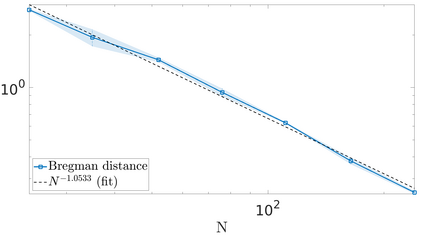
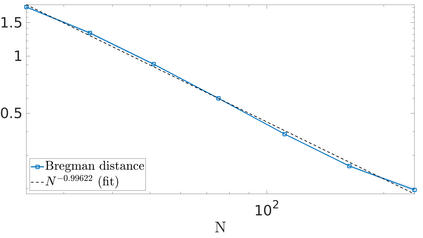
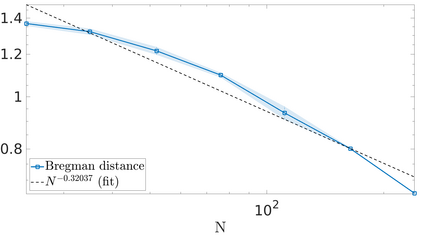
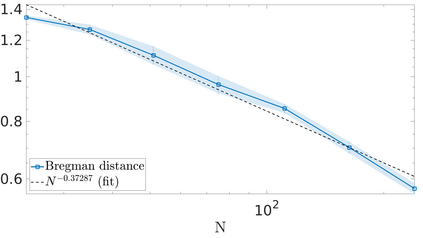
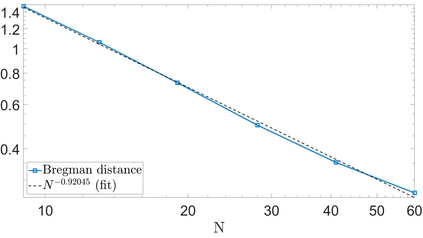
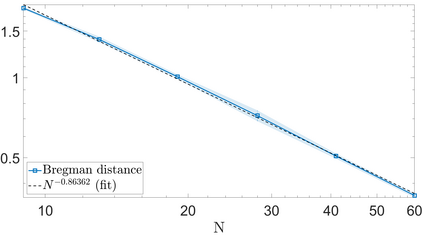
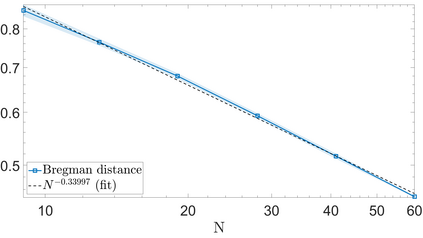
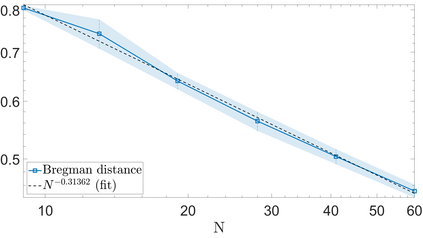
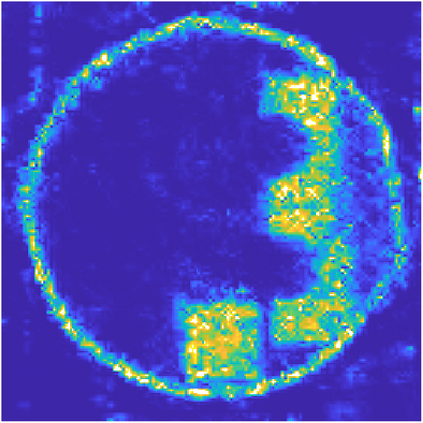
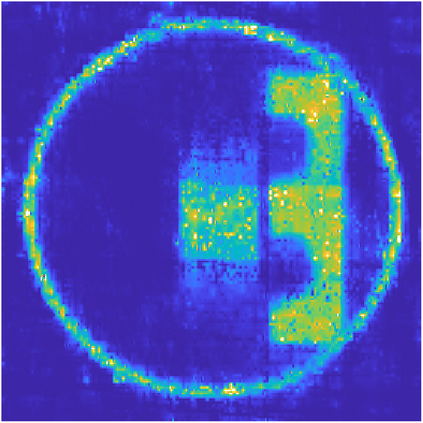
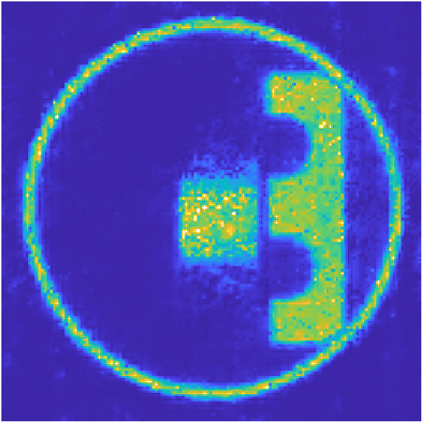
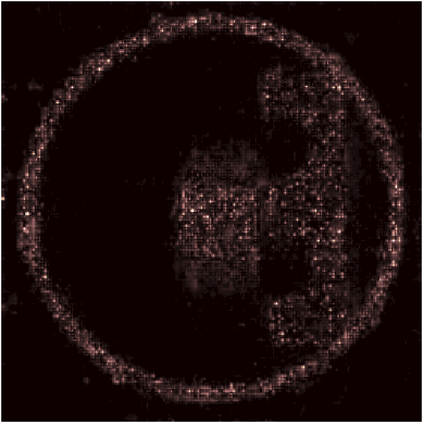
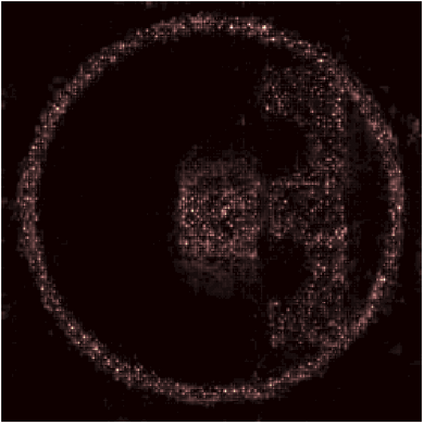
We propose a variational regularization approach based on cylindrical shearlets to deal with dynamic imaging problems, with dynamic tomography as guiding example. The idea is that the mismatch term essentially integrates a sequence of separable, static problems, while the regularization term sees the non-stationary target as a spatio-temporal object. We motivate this approach by showing that cylindrical shearlets provide optimally sparse approximations for the class of cartoon-like videos, i.e., a class of functions useful to model spatio-temporal image sequences and videos, which we introduce extending the classic notion of cartoon-like images. To formulate our regularization model, we define cylindrical shearlet smoothness spaces, which is pivotal to obtain suitable embeddings in functional spaces. To complete our analysis, we prove that the proposed regularization strategy is well-defined, the solution of the minimisation problem exists and is unique (for $ p > 1$). Furthermore, we provide convergence rates (in terms of the symmetric Bregman distance) under deterministic and random noise conditions, and within the context of statistical inverse learning. We numerically validate our theoretical results using both simulated and measured dynamic tomography data, showing that our approach leads to a practical and robust reconstruction strategy.
翻译:暂无翻译