Deterministic limit of temporal difference reinforcement learning for stochastic games

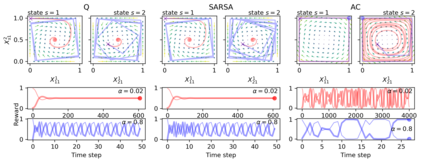
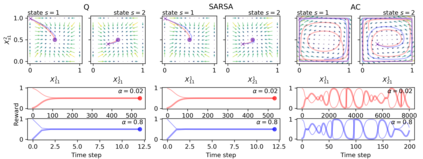
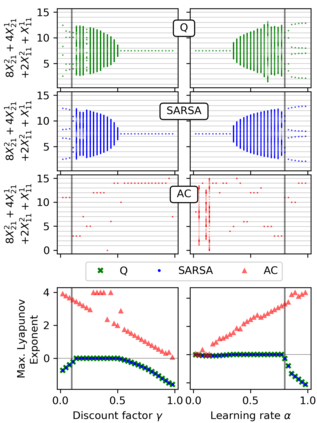
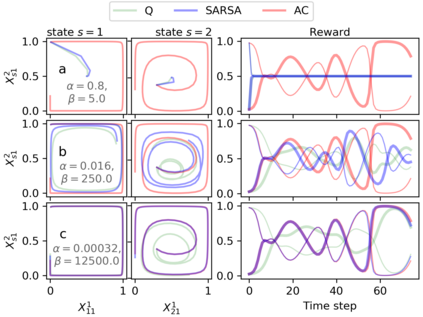
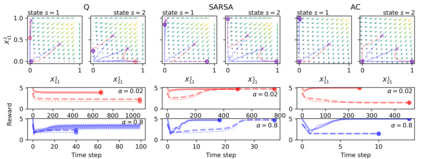
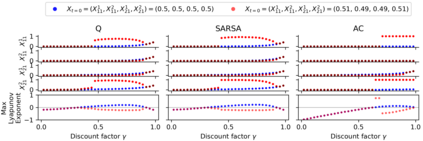
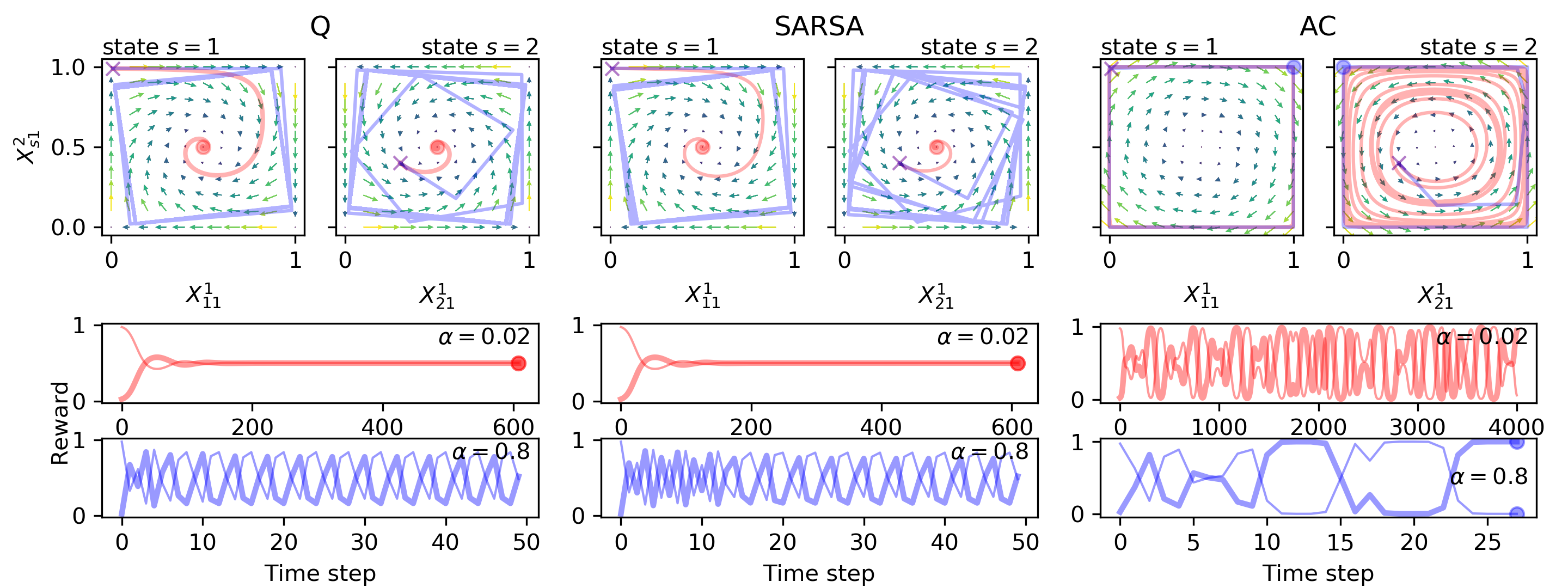
Reinforcement learning in multi-agent systems has been studied in the fields of economic game theory, artificial intelligence and statistical physics by developing an analytical understanding of the learning dynamics (often in relation to the replicator dynamics of evolutionary game theory). However, the majority of these analytical studies focuses on repeated normal form games, which only have a single environmental state. Environmental dynamics, i.e. changes in the state of an environment affecting the agents' payoffs has received less attention, lacking a universal method to obtain deterministic equations from established multi-state reinforcement learning algorithms. In this work we present a novel methodology to derive the deterministic limit resulting from an interaction-adaptation time scales separation of a general class of reinforcement learning algorithms, called temporal difference learning. This form of learning is equipped to function in more realistic multi-state environments by using the estimated value of future environmental states to adapt the agent's behavior. We demonstrate the potential of our method with the three well established learning algorithms Q learning, SARSA learning and Actor-Critic learning. Illustrations of their dynamics on two multi-agent, multi-state environments reveal a wide range of different dynamical regimes, such as convergence to fixed points, limit cycles and even deterministic chaos.