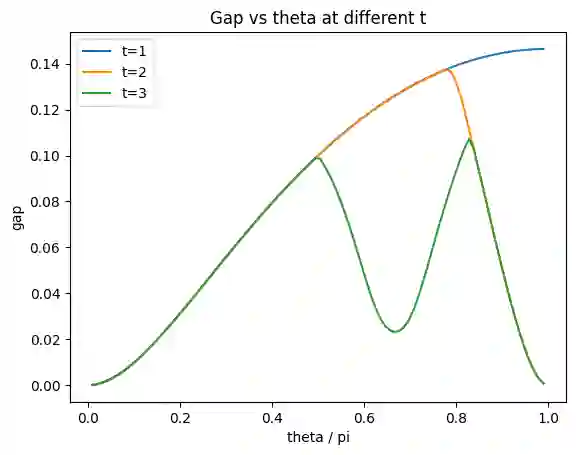
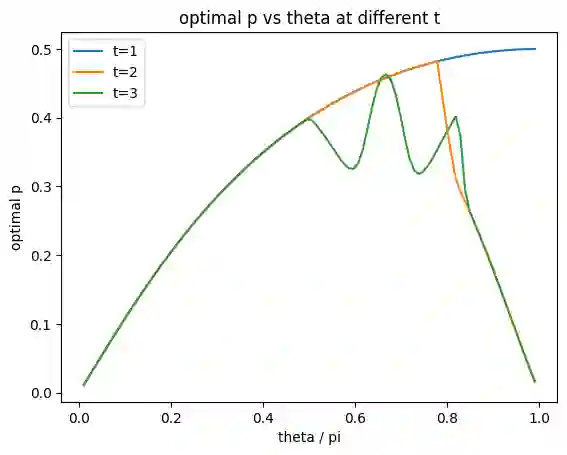
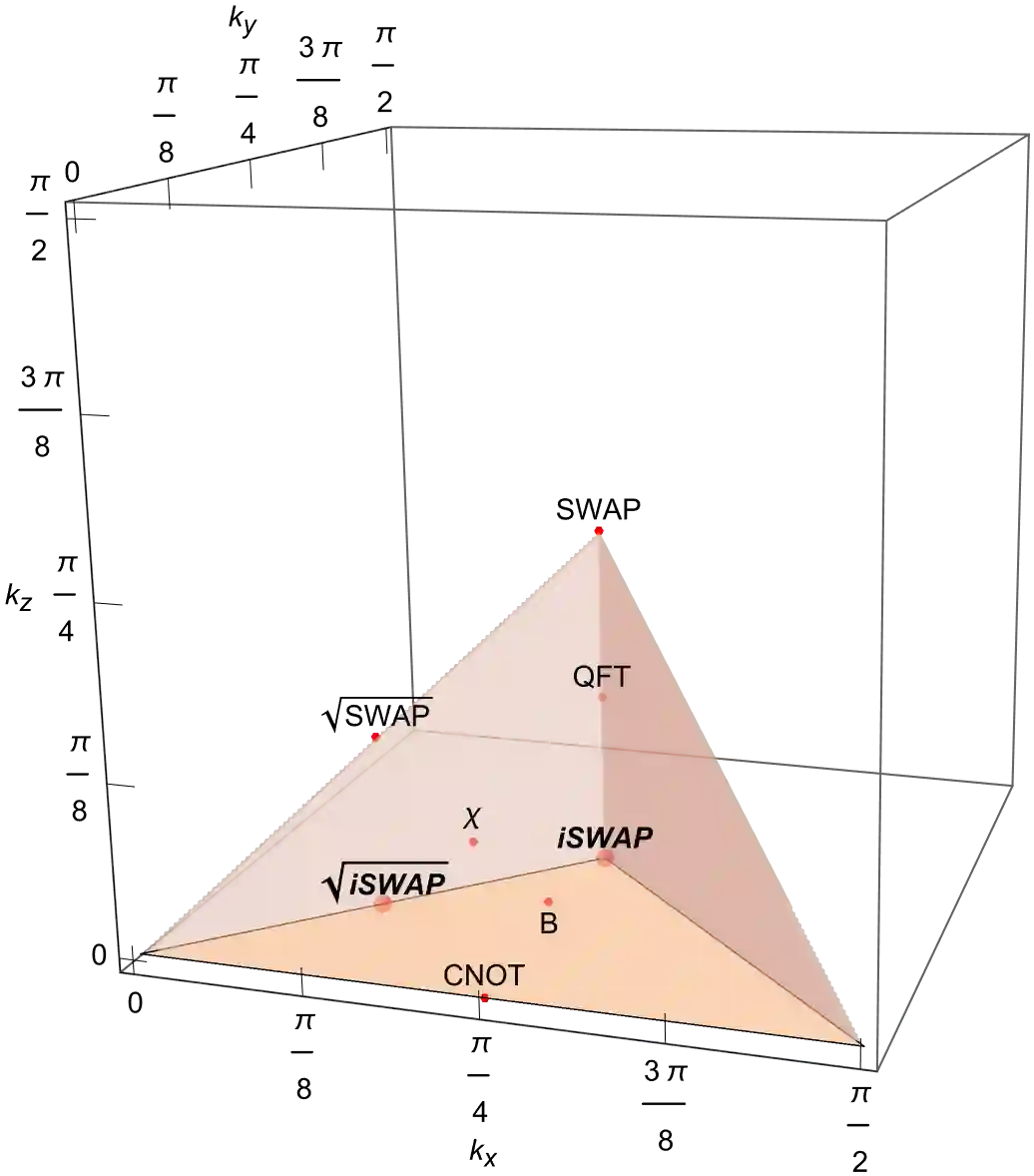
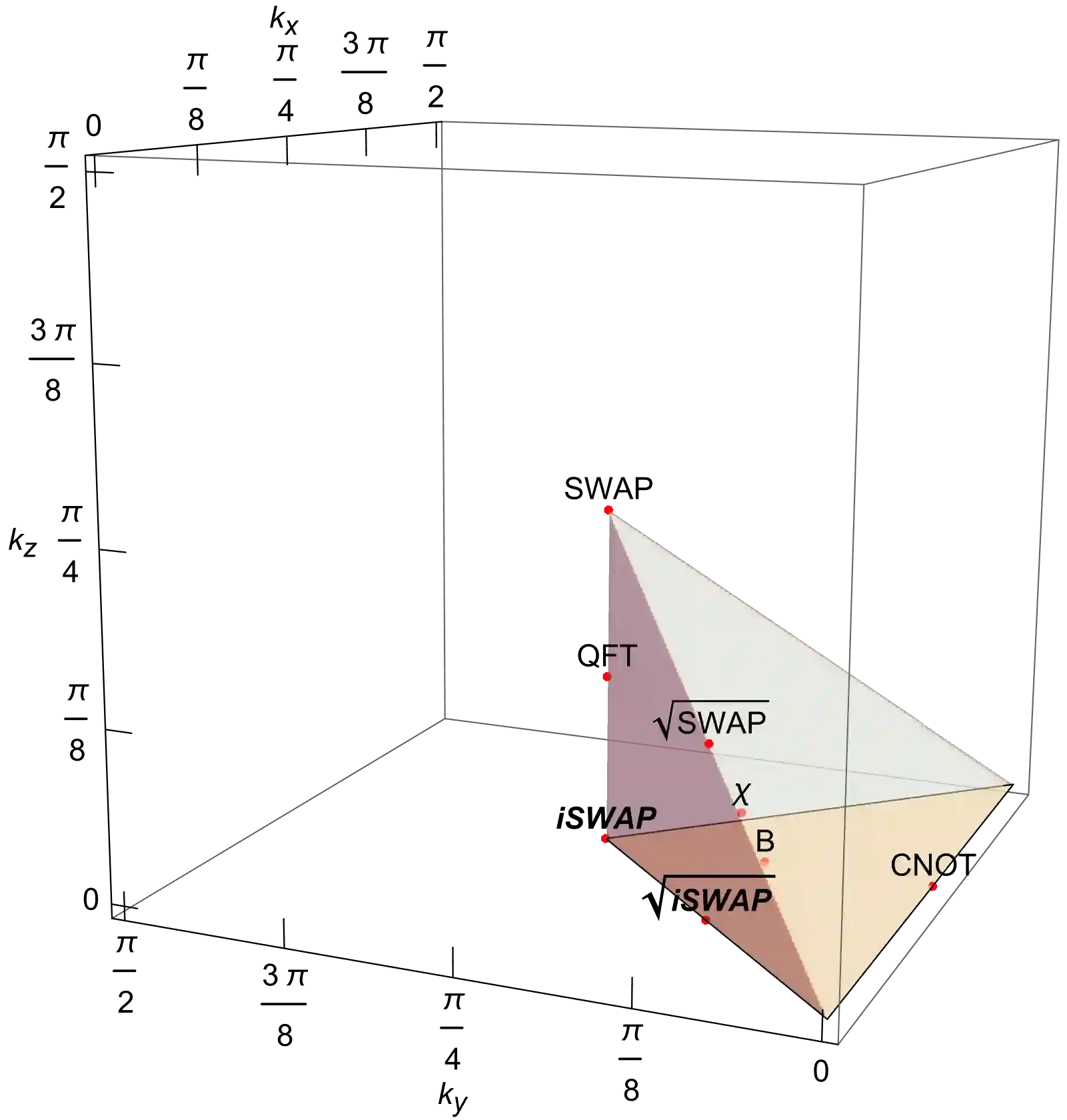
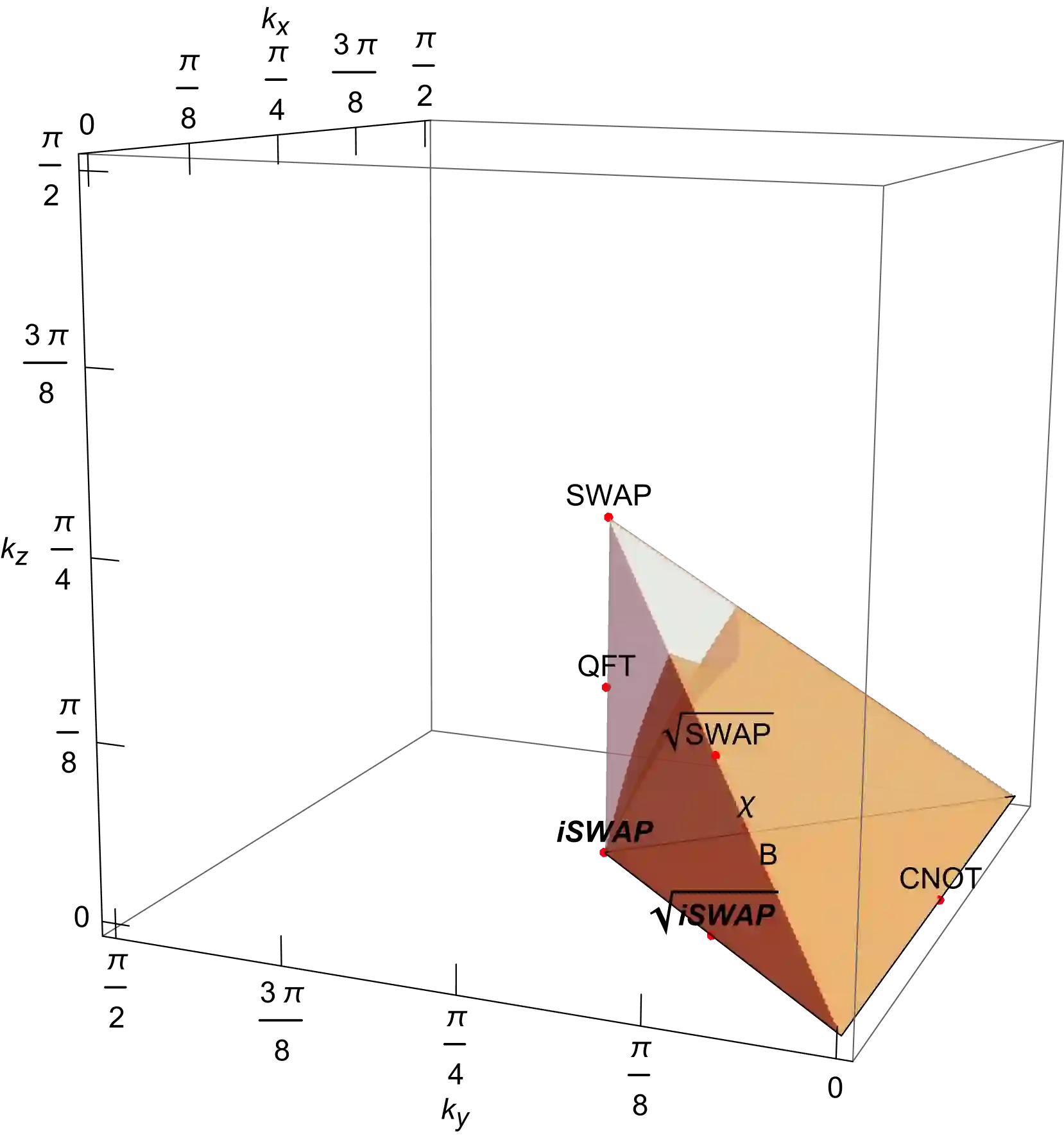
We consider quantum circuit models where the gates are drawn from arbitrary gate ensembles given by probabilistic distributions over certain gate sets and circuit architectures, which we call stochastic quantum circuits. Of main interest in this work is the speed of convergence of stochastic circuits with different gate ensembles and circuit architectures to unitary t-designs. A key motivation for this theory is the varying preference for different gates and circuit architectures in different practical scenarios. In particular, it provides a versatile framework for devising efficient circuits for implementing $t$-designs and relevant applications including random circuit and scrambling experiments, as well as benchmarking the performance of gates and circuit architectures. We examine various important settings in depth. A key aspect of our study is an "ironed gadget" model, which allows us to systematically evaluate and compare the convergence efficiency of entangling gates and circuit architectures. Particularly notable results include i) gadgets of two-qubit gates with KAK coefficients $\left(\frac{\pi}{4}-\frac{1}{8}\arccos(\frac{1}{5}),\frac{\pi}{8},\frac{1}{8}\arccos(\frac{1}{5})\right)$ (which we call $\chi$ gates) directly form exact 2- and 3-designs; ii) the iSWAP gate family achieves the best efficiency for convergence to 2-designs under mild conjectures with numerical evidence, even outperforming the Haar-random gate, for generic many-body circuits; iii) iSWAP + complete graph achieve the best efficiency for convergence to 2-designs among all graph circuits. A variety of numerical results are provided to complement our analysis. We also derive robustness guarantees for our analysis against gate perturbations. Additionally, we provide cursory analysis on gates with higher locality and found that the Margolus gate outperforms various other well-known gates.
翻译:暂无翻译