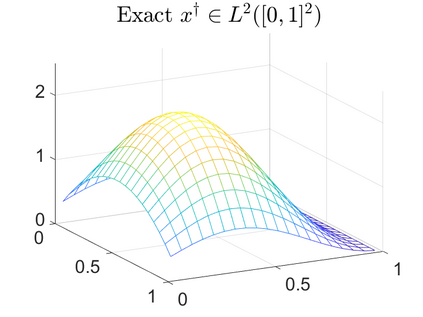
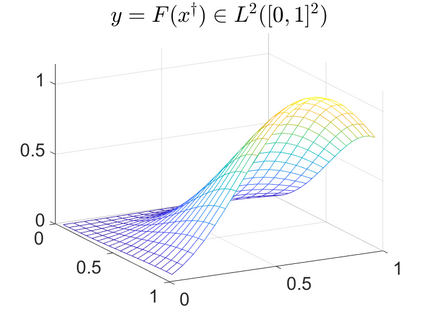
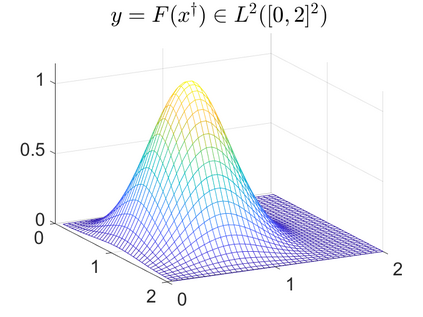
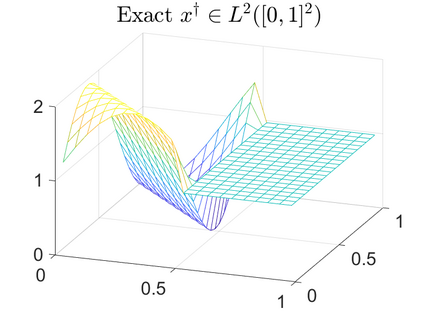
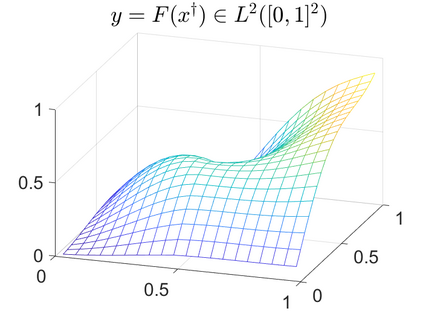
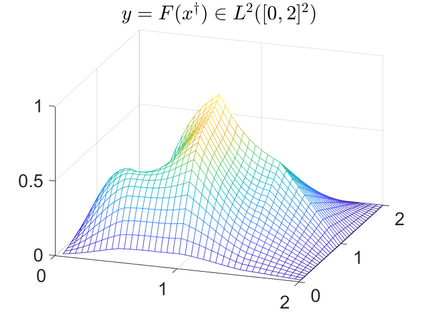
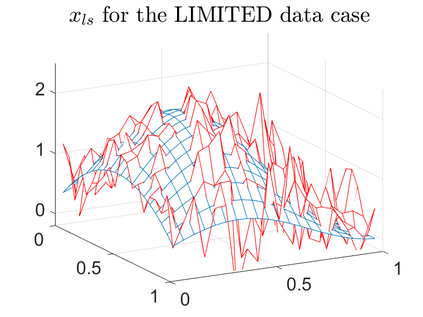
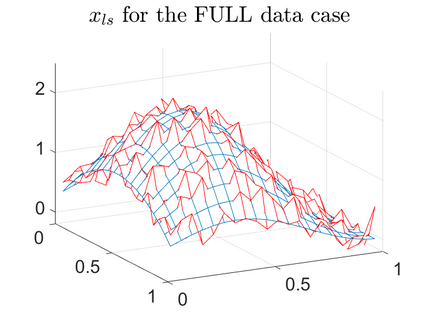
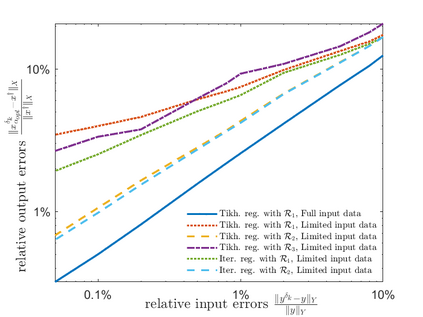
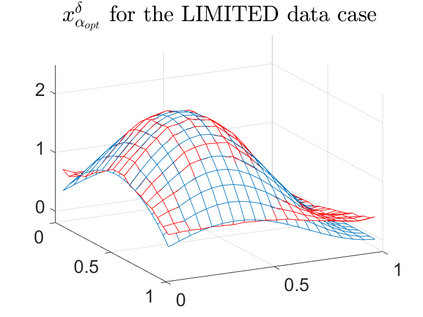
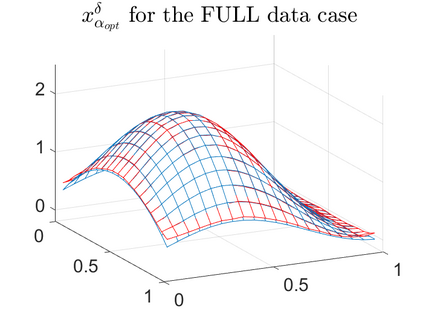
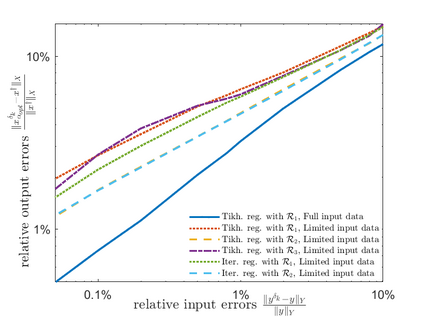
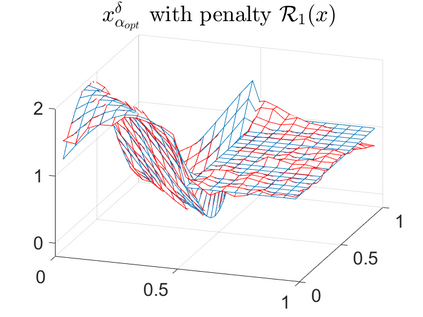
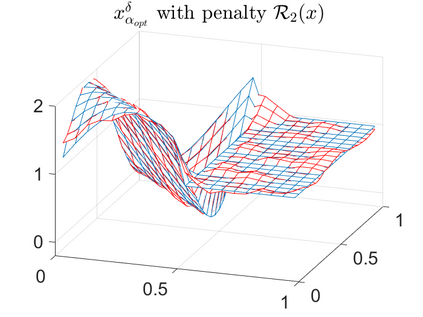
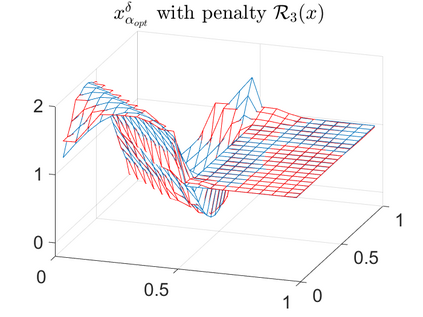
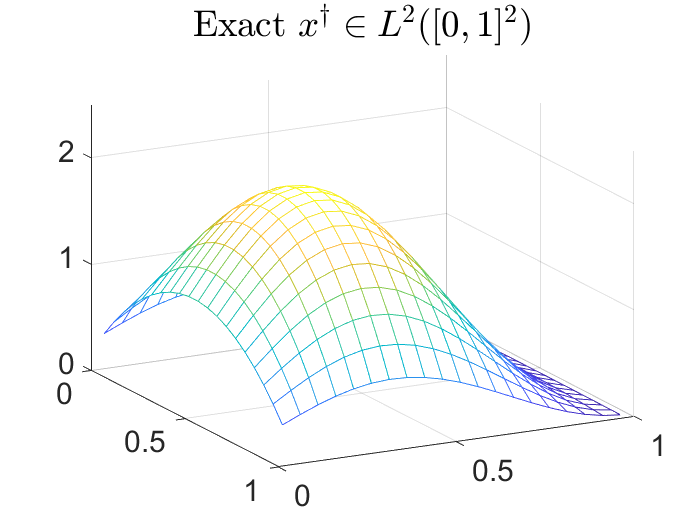
There is extensive mathematical literature on the inverse problem of deautoconvolution for a function with support in the unit interval $[0,1] \subset \mathbb R$, but little is known about the multidimensional situation. This article tries to fill this gap with analytical and numerical studies on the reconstruction of a real function of two real variables over the unit square from observations of its autoconvolution on $[0,2]^2 \subset \mathbb R^2$ (full data case) or on $[0,1]^2$ (limited data case). In an $L^2$-setting, twofoldness and uniqueness assertions are proven for the deautoconvolution problem in 2D. Moreover, its ill-posedness is characterized and illustrated. Extensive numerical case studies give an overview of the behaviour of stable approximate solutions to the two-dimensional deautoconvolution problem obtained by Tikhonov-type regularization with different penalties and the iteratively regularized Gauss-Newton method.
翻译:在单位间隔 $0,1,\ subset \ mathbb R$ 支持函数的反自动变换问题方面有大量数学文献,但对于多维情况却知之甚少。文章试图用分析和数字研究来填补这一空白,从对单位正方形上两个实际变数的真正变数的重建中观察其自动变换 $2,2,2,2 \ subthb R/2$ (完整数据案例) 或 $0,1,1,2美元 (有限数据案例) 。在2D 的自动变换问题中,2美元设定、双元和独特性主张得到了证明。此外,其错误的特性和说明也得到了广泛数字案例研究的概括,其中概述了用不同惩罚和迭代法固定高斯-纽顿法获得的对Tikhonov 型变形变形变形变形变形变形变形问题稳定近近解决方案的行为。