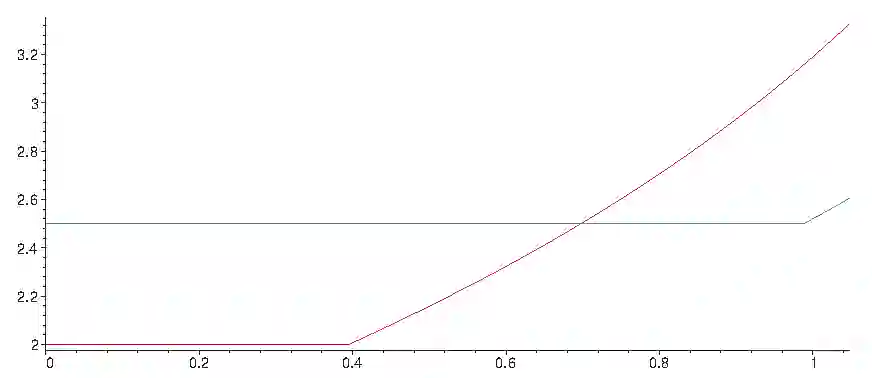
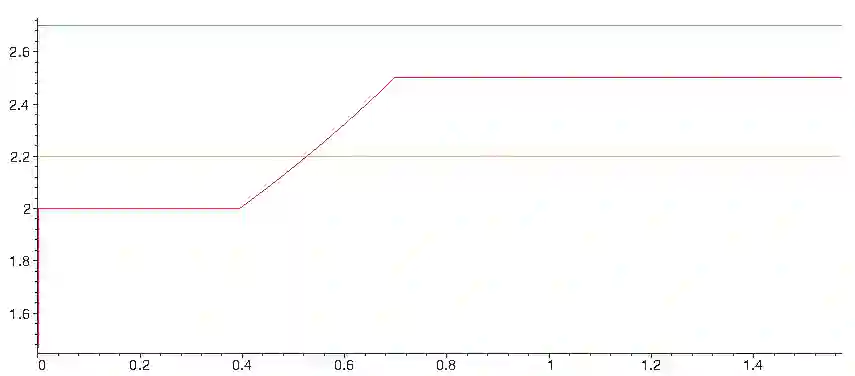
We consider the online two-dimensional vector packing problem, showing a lower bound of $11/5$ on the competitive ratio of any {\sc AnyFit} strategy for the problem. We provide strategies with competitive ratio $\max\!\left\{2,6\big/\big(1+3\tan(\pi/4-\gamma/2)\big)+\epsilon\right\}$ and logarithmic advice, for any instance where all the input vectors are restricted to have angles in the range $[\pi/4-\gamma/2,\pi/4+\gamma/2]$, for $0\leq\gamma<\pi/3$ and $\max\left\{5/2,4\big/\big(1+2\tan(\pi/4-\gamma/2)\big)+\epsilon\right\}$ and logarithmic advice, for any instance where all the input vectors are restricted to have angles in the range $[\pi/4-\gamma/2,\pi/4+\gamma/2]$, for $0\leq\gamma\leq\pi/3$. In addition, we give a $5/2$-competitive strategy also using logarithmic advice for the unrestricted vectors case. These results should be contrasted to the currently best competitive strategy, FirstFit, having competitive ratio~$27/10$.
翻译:我们考虑在线二维矢量包装问题, 显示任何 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 在线双维矢量包装问题, 在任何 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 的竞争性比例上, 我们提供的战略是: 1+3\ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 选择 选择 选择 选择 选择 / / / /, 我们, 我们, $ $ $, ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ / / ~ / / / / / / ~ / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / /