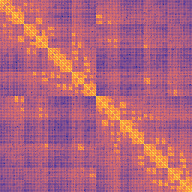
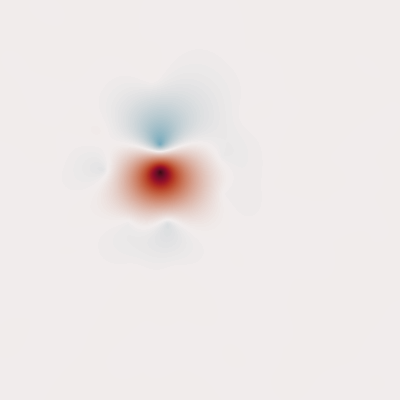
Nonstationary Gaussian process models can capture complex spatially varying dependence structures in spatial datasets. However, the large number of observations in modern datasets makes fitting such models computationally intractable with conventional dense linear algebra. In addition, derivative-free or even first-order optimization methods can be slow to converge when estimating many spatially varying parameters. We present here a computational framework that couples an algebraic block-diagonal plus low-rank covariance matrix approximation with stochastic trace estimation to facilitate the efficient use of second-order solvers for maximum likelihood estimation of Gaussian process models with many parameters. We demonstrate the effectiveness of these methods by simultaneously fitting 192 parameters in the popular nonstationary model of Paciorek and Schervish using 107,600 sea surface temperature anomaly measurements.
翻译:在空间数据集中,非静止高斯进程模型可以捕捉到复杂的空间上差异的依附结构,然而,现代数据集中观测的数量之多,使得这些模型在计算上难以与传统的密度线性代数相匹配;此外,在估计许多空间差异的参数时,无衍生物或甚至一阶优化方法可能比较缓慢,无法汇合;我们在此提出一个计算框架,将代数区块对角加上低位共变矩阵近似值与随机微量估计结合起来,以便于高效使用二阶求解器对带有多种参数的高斯进程模型进行最大可能性估计;我们通过利用107 600海面温度异常测量,同时将普西罗雷克和舍尔维什流行非静止模型中的192项参数相匹配,以显示这些方法的有效性。