On Greedy Approaches to Hierarchical Aggregation

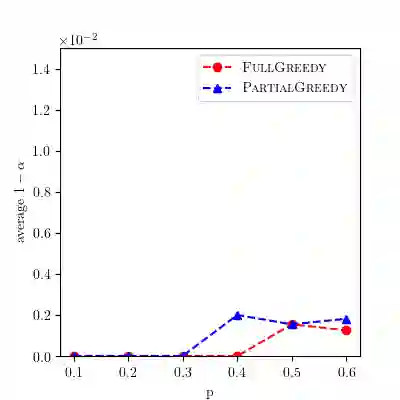
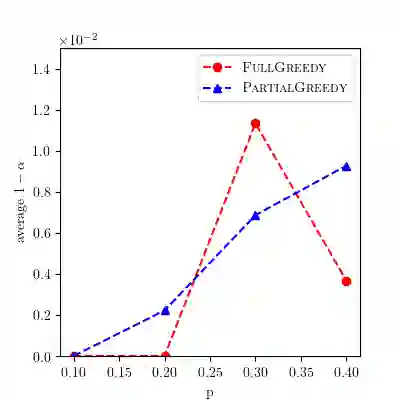
We analyze greedy algorithms for the Hierarchical Aggregation (HAG) problem, a strategy introduced in [Jia et al., KDD 2020] for speeding up learning on Graph Neural Networks (GNNs). The idea of HAG is to identify and remove redundancies in computations performed when training GNNs. The associated optimization problem is to identify and remove the most redundancies. Previous work introduced a greedy approach for the HAG problem and claimed a 1-1/e approximation factor. We show by example that this is not correct, and one cannot hope for better than a 1/2 approximation factor. We prove that this greedy algorithm does satisfy some (weaker) approximation guarantee, by showing a new connection between the HAG problem and maximum matching problems in hypergraphs. We also introduce a second greedy algorithm which can out-perform the first one, and we show how to implement it efficiently in some parameter regimes. Finally, we introduce some greedy heuristics that are much faster than the above greedy algorithms, and we demonstrate that they perform well on real-world graphs.