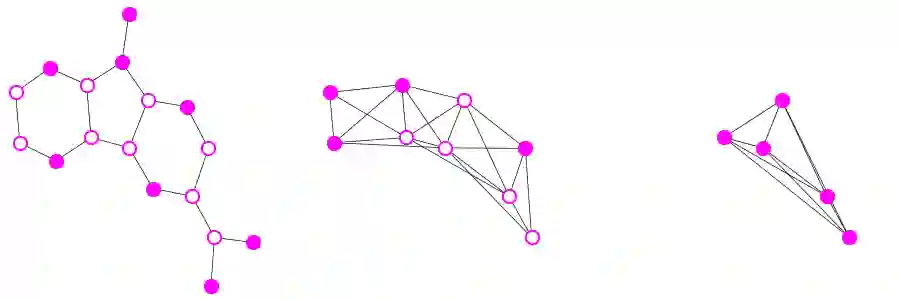
Hierarchical abstractions are a methodology for solving large-scale graph problems in various disciplines. Coarsening is one such approach: it generates a pyramid of graphs whereby the one in the next level is a structural summary of the prior one. With a long history in scientific computing, many coarsening strategies were developed based on mathematically driven heuristics. Recently, resurgent interests exist in deep learning to design hierarchical methods learnable through differentiable parameterization. These approaches are paired with downstream tasks for supervised learning. In practice, however, supervised signals (e.g., labels) are scarce and are often laborious to obtain. In this work, we propose an unsupervised approach, coined OTCoarsening, with the use of optimal transport. Both the coarsening matrix and the transport cost matrix are parameterized, so that an optimal coarsening strategy can be learned and tailored for a given set of graphs. We demonstrate that the proposed approach produces meaningful coarse graphs and yields competitive performance compared with supervised methods for graph classification and regression.
翻译:分层抽象学是解决不同学科的大型图表问题的一种方法。 粗略学是这样一种方法: 它产生一个图形金字塔, 下一层的图形是前一层的结构摘要。 由于科学计算的历史悠久, 许多粗糙的策略都是根据数学驱动的杂技学来制定的。 最近, 深层学习以设计通过不同参数化可以学习的等级方法方面的兴趣死灰复燃。 这些方法与下游任务相配, 用于监督学习。 然而, 在实践中, 受监督的信号( 如标签) 稀少, 并且往往难以获得。 在这项工作中, 我们提出一种不受监督的方法, 以优化的运输方式催化 OTCoarse 。 粗略矩阵和运输成本矩阵都具有参数化作用, 从而可以学习最佳的粗糙策略, 并针对特定的一组图表进行量身定制。 我们证明, 拟议的方法产生了有意义的粗糙的图表, 并产生与受监督的图表分类和回归方法相比, 具有竞争性的性表现。