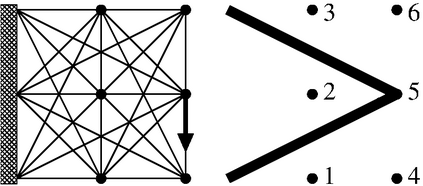
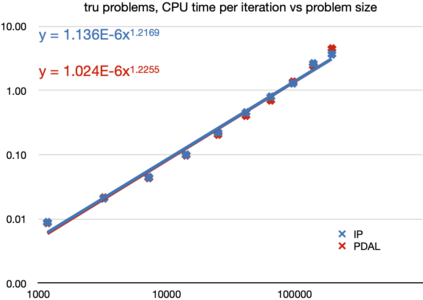
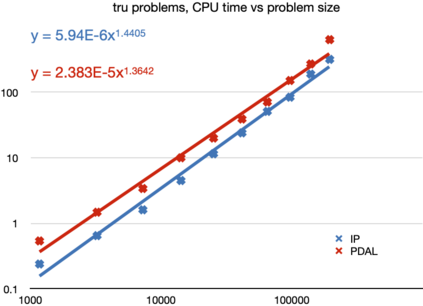
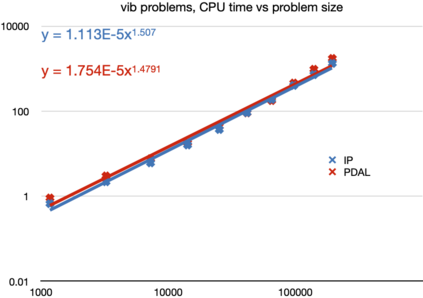
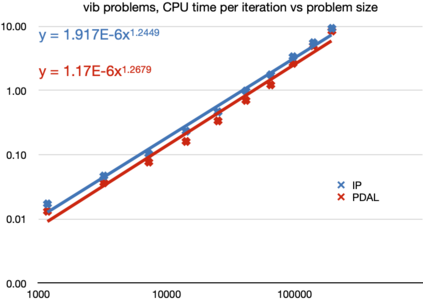
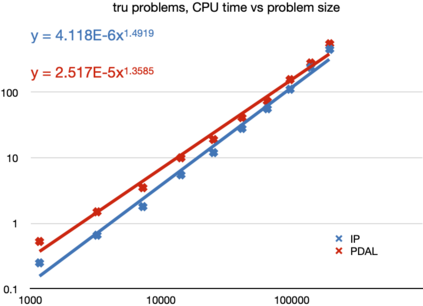
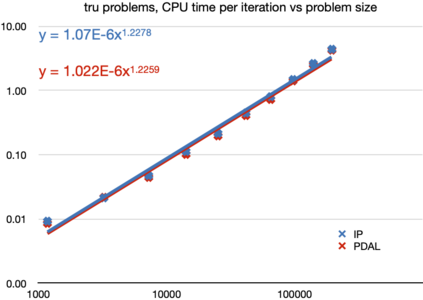
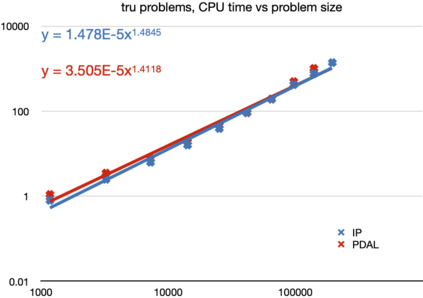
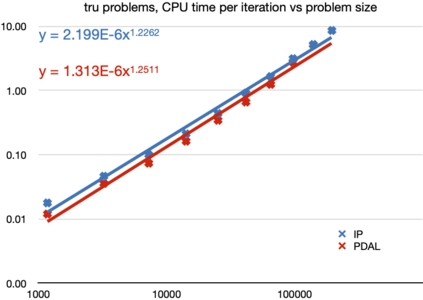
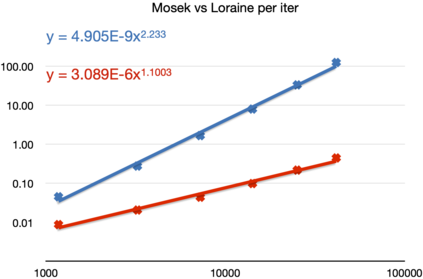
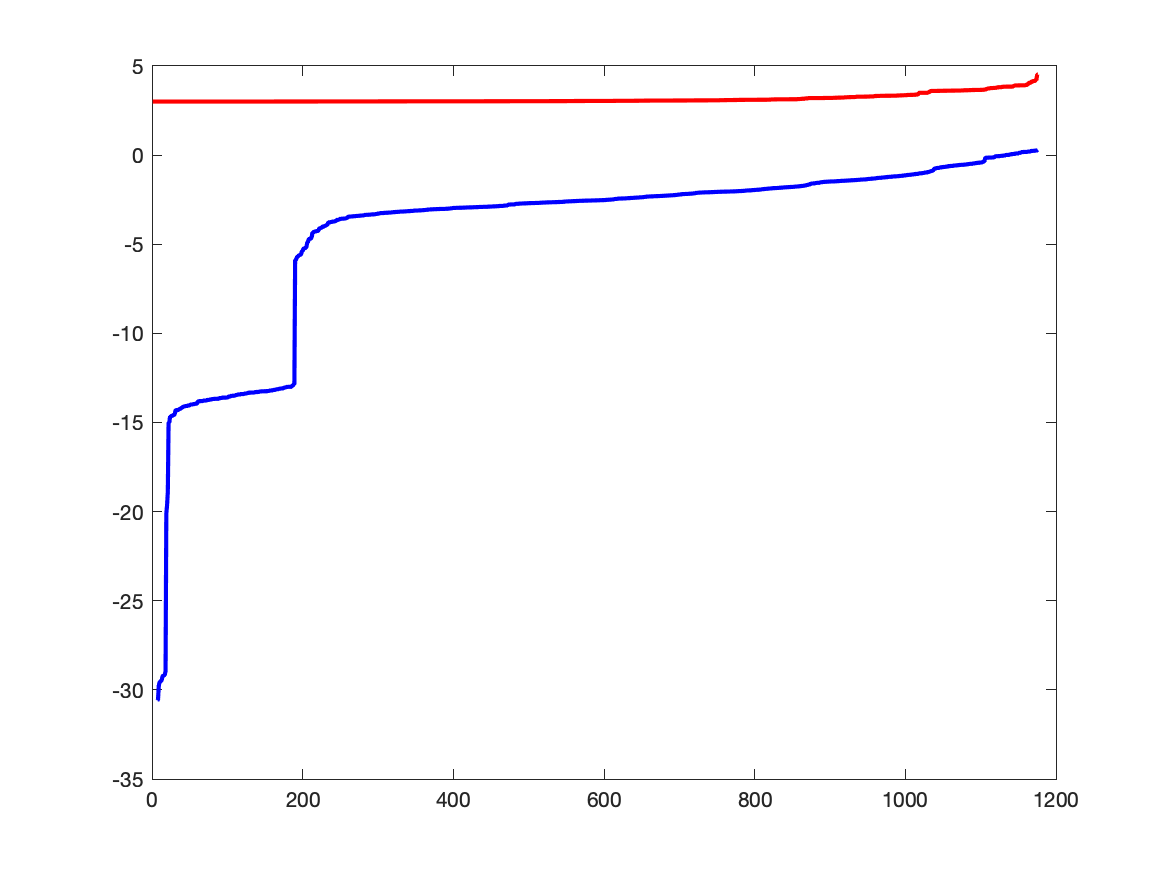
The aim of this paper is to solve large-and-sparse linear Semidefinite Programs (SDPs) with low-rank solutions. We propose to use a preconditioned conjugate gradient method within second-order SDP algorithms and introduce a new efficient preconditioner fully utilizing the low-rank information. We demonstrate that the preconditioner is universal, in the sense that it can be efficiently used within a standard interior-point algorithm, as well as a newly developed primal-dual penalty method. The efficiency is demonstrated by numerical experiments using the truss topology optimization problems of growing dimension.
翻译:本文的目的是用低级解决方案解决大而小的线性线性半成品程序(SDPs)问题,我们提议在二级SDP算法中使用一个先决条件的同梯度方法,并引入一个充分利用低级信息的新的高效先决条件。我们证明先决条件是普遍性的,即可以在标准的内点算法和新开发的初等双罚法方法中有效使用。通过使用日益扩大的Turuss 地形优化问题进行数字实验,可以证明效率。