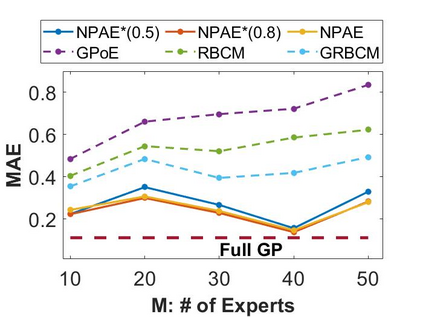
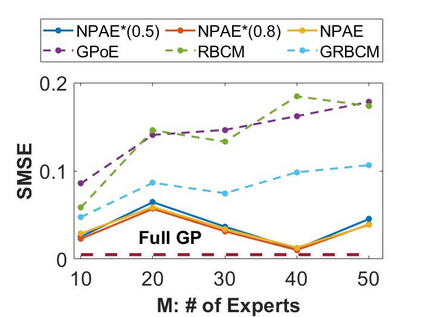
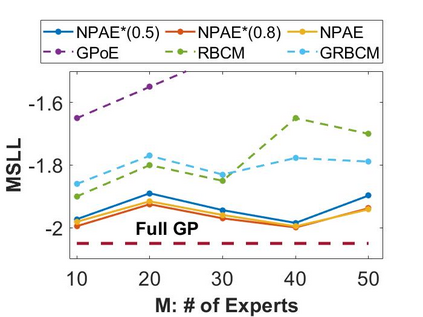
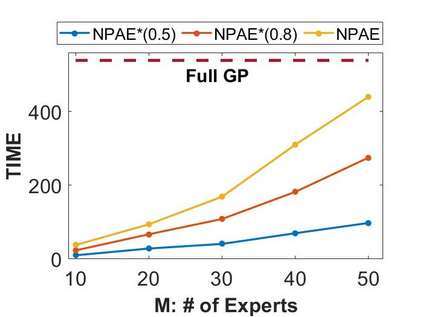
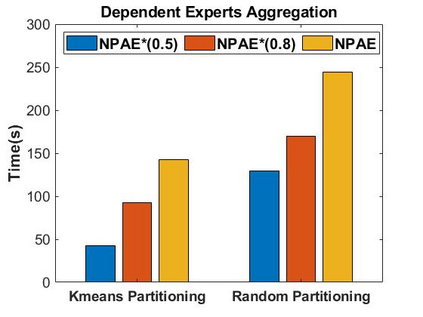
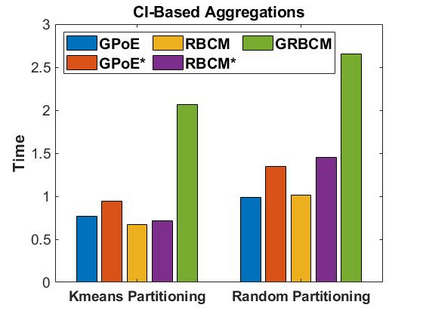
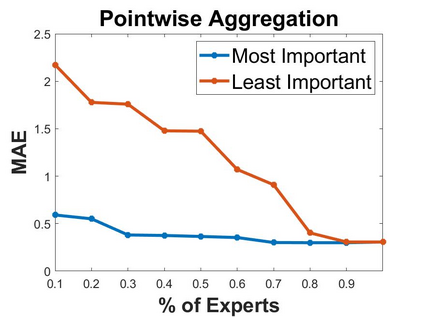
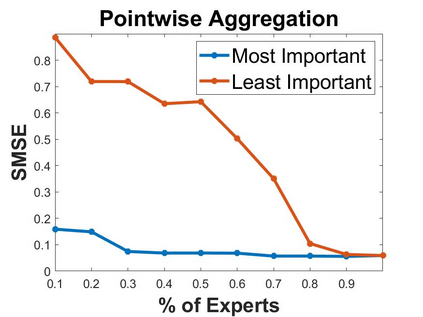
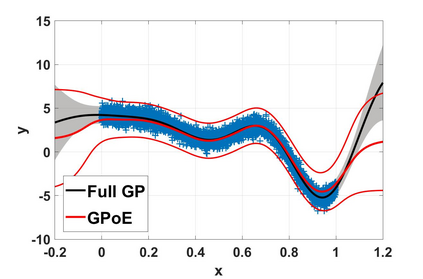
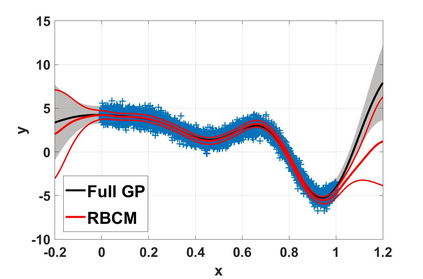
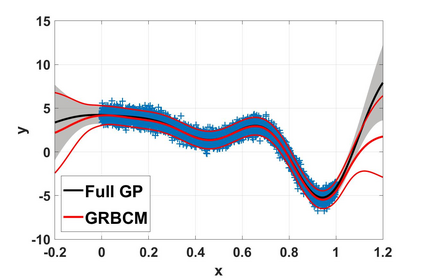
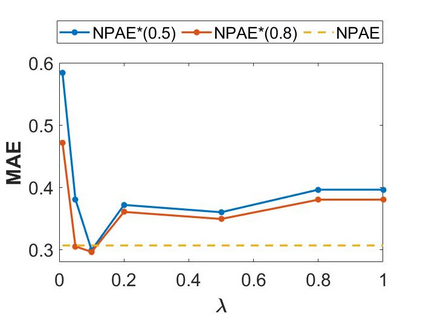
Local approximations are popular methods to scale Gaussian processes (GPs) to big data. Local approximations reduce time complexity by dividing the original dataset into subsets and training a local expert on each subset. Aggregating the experts' prediction is done assuming either conditional dependence or independence between the experts. Imposing the \emph{conditional independence assumption} (CI) between the experts renders the aggregation of different expert predictions time efficient at the cost of poor uncertainty quantification. On the other hand, modeling dependent experts can provide precise predictions and uncertainty quantification at the expense of impractically high computational costs. By eliminating weak experts via a theory-guided expert selection step, we substantially reduce the computational cost of aggregating dependent experts while ensuring calibrated uncertainty quantification. We leverage techniques from the literature on undirected graphical models, using sparse precision matrices that encode conditional dependencies between experts to select the most important experts. Moreov
翻译:本地近似是将高斯进程(GPs)与大数据相比的常用方法。 本地近似通过将原始数据集分成子集,并培训当地每组专家来降低时间复杂性。 将专家的预测汇总,假设专家之间的有条件依赖性或独立性。 在专家之间实施 \ emph{ 有条件独立假设} (CI) 使不同专家预测的汇总时间效率高,但代价是不确定性的量化差。 另一方面, 模拟依赖专家可以提供精确的预测和不确定性的量化,而牺牲不切实际的高计算成本。 通过理论引导的专家选择步骤消除薄弱的专家,我们大幅降低依赖专家集成的计算成本,同时确保校准的不确定性量化。 我们利用文献中的非定向图形模型技术,使用分散的精确矩阵将专家之间的有条件依赖性编码用于选择最重要的专家。 Moreov 。