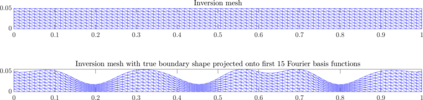
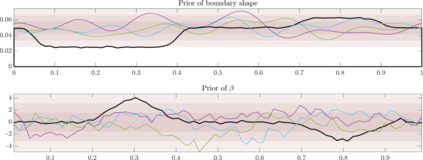
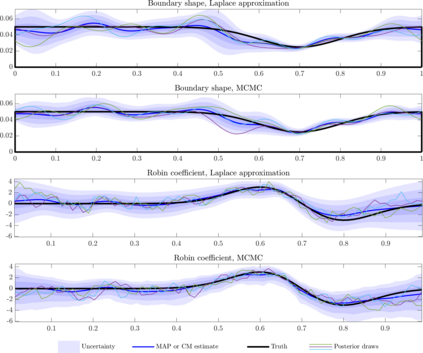
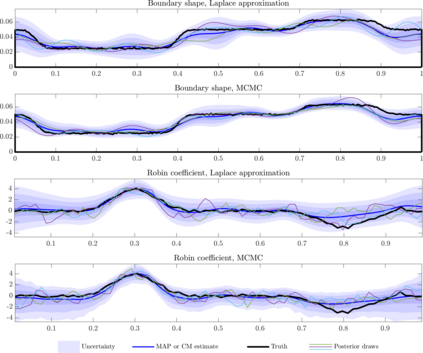
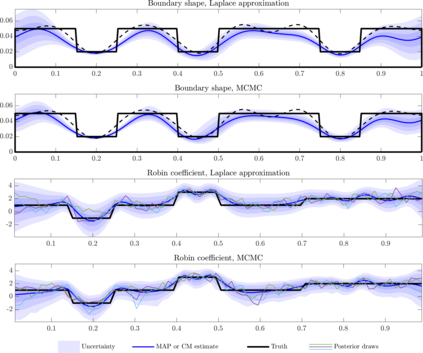
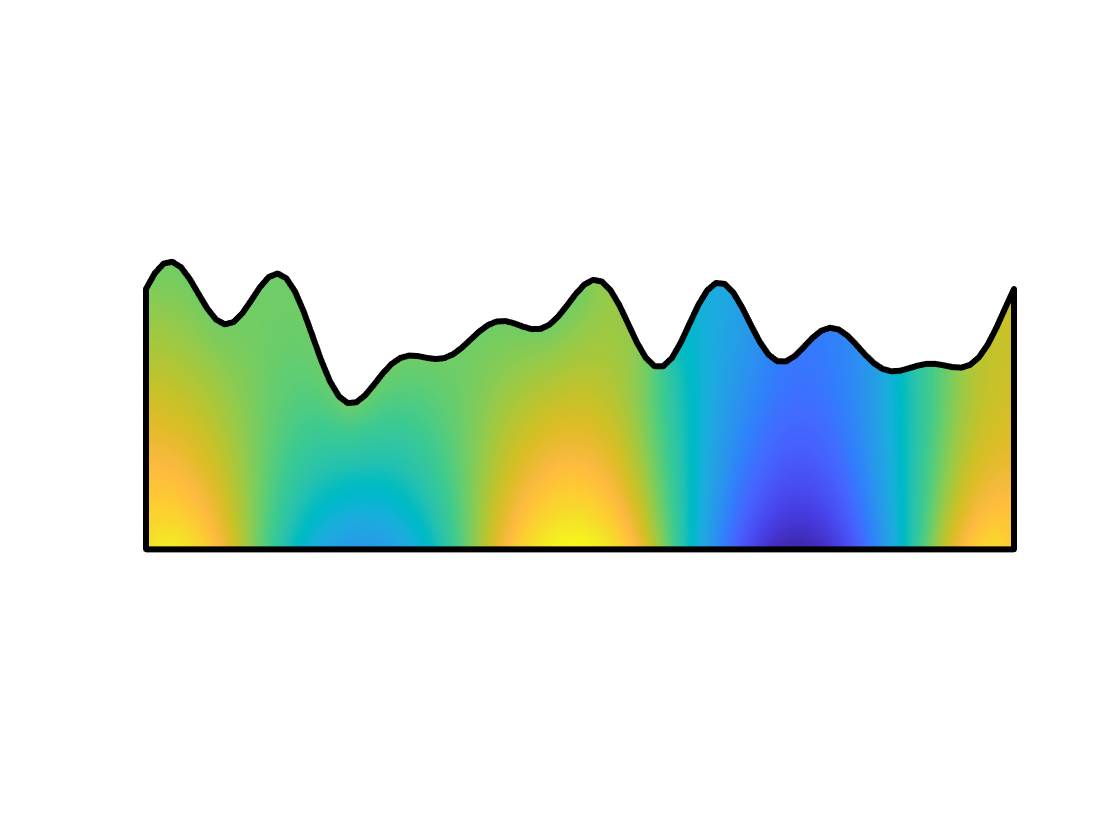
We consider the problem of simultaneously inferring the heterogeneous coefficient field for a Robin boundary condition on an inaccessible part of the boundary along with the shape of the boundary for the Poisson problem. Such a problem arises in, for example, corrosion detection, and thermal parameter estimation. We carry out both linearised uncertainty quantification, based on a local Gaussian approximation, and full exploration of the joint posterior using Markov chain Monte Carlo (MCMC) sampling. By exploiting a known invariance property of the Poisson problem, we are able to circumvent the need to re-mesh as the shape of the boundary changes. The linearised uncertainty analysis presented here relies on a local linearisation of the parameter-to-observable map, with respect to both the Robin coefficient and the boundary shape, evaluated at the maximum a posteriori (MAP) estimates. Computation of the MAP estimate is carried out using the Gauss-Newton method. On the other hand, to explore the full joint posterior we use the Metropolis-adjusted Langevin algorithm (MALA), which requires the gradient of the log-posterior. We thus derive both the Fr\'{e}chet derivative of the solution to the Poisson problem with respect to the Robin coefficient and the boundary shape, and the gradient of the log-posterior, which is efficiently computed using the so-called adjoint approach. The performance of the approach is demonstrated via several numerical experiments with simulated data.
翻译:我们考虑的问题是,同时根据无法进入的边界部分以及波瓦松问题的边界形状,推算罗宾边界条件的混杂系数场,同时推算关于罗宾边界条件的混杂系数场,以及波瓦松问题的边界形状。例如,在腐蚀探测和热参数估计方面出现这样的问题。我们根据当地的戈萨近似值进行线性不确定性量化,并使用马科夫链-蒙特卡洛(MCMC)抽样全面探索联合后继器。通过利用波瓦松问题已知的偏差属性,我们能够绕过重塑作为边界变化形状的需要。这里提出的线性不确定性分析取决于参数对可观测的地图的局部线性化,关于罗宾系数和边界形状的线性定线性化,以最高后验估计值(MAP)为基础进行评估。利用高斯-牛顿方法对地中海行动计划估计值进行计算。另一方面,我们利用Metopolis-andio 调制朗埃文算算法(MALA)的完全联合方法,这需要对可观测到可观测的参数和边界形状的梯值的梯值的梯度的梯度的梯度。因此,我们用了对正正变的正位的轨道的轨道的轨道的轨道的轨道的精确度,我们用了对正平比的轨道的轨道的轨道的轨道的测算。