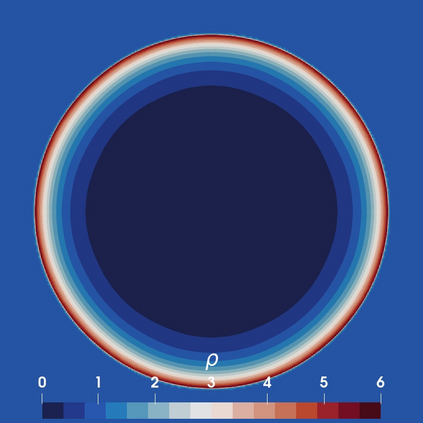
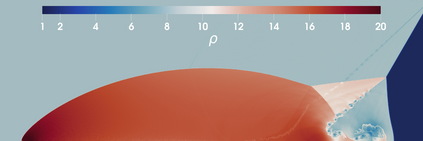
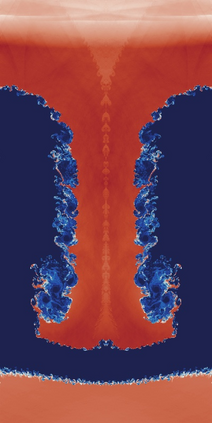
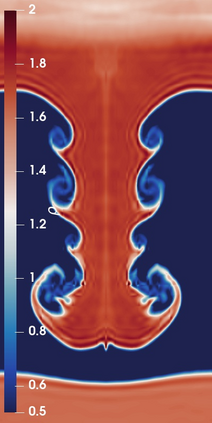
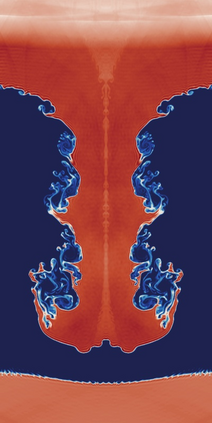
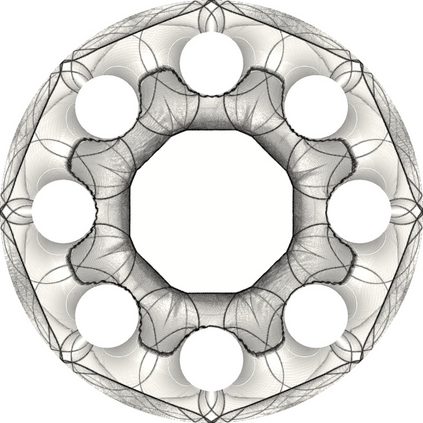
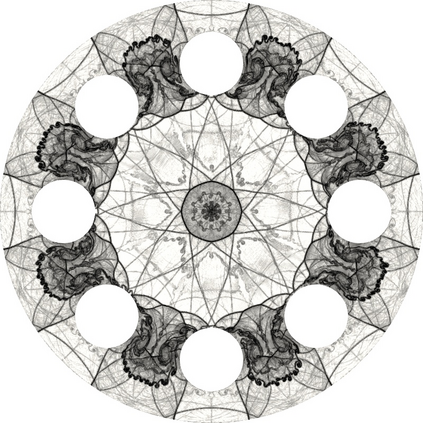
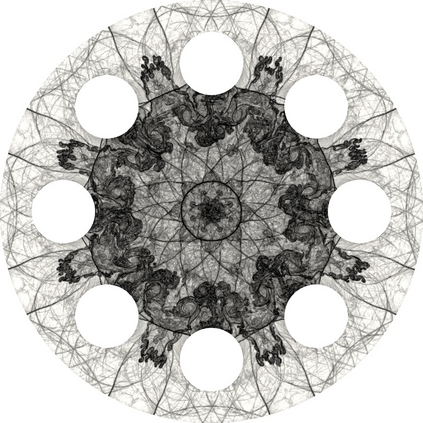
The use of limiting methods for high-order numerical approximations of hyperbolic conservation laws generally requires defining an admissible region/bounds for the solution. In this work, we present a novel approach for computing solution bounds and limiting for the Euler equations through the kinetic representation provided by the Boltzmann equation, which allows for extending limiters designed for linear advection directly to the Euler equations. Given an arbitrary set of solution values to compute bounds over (e.g., numerical stencil) and a desired linear advection limiter, the proposed approach yields an analytic expression for the admissible region of particle distribution function values, which may be numerically integrated to yield a set of bounds for the density, momentum, and total energy. These solution bounds are shown to preserve positivity of density/pressure/internal energy and, when paired with a limiting technique, can robustly resolve strong discontinuities while recovering high-order accuracy in smooth regions without any ad hoc corrections (e.g., relaxing the bounds). This approach is demonstrated in the context of an explicit unstructured high-order discontinuous Galerkin/flux reconstruction scheme for a variety of difficult problems in gas dynamics, including cases with extreme shocks and shock-vortex interactions. Furthermore, this work presents a foundation for limiting techniques for more complex macroscopic governing equations that can be derived from an underlying kinetic representation for which admissible solution bounds are not well-understood.
翻译:暂无翻译