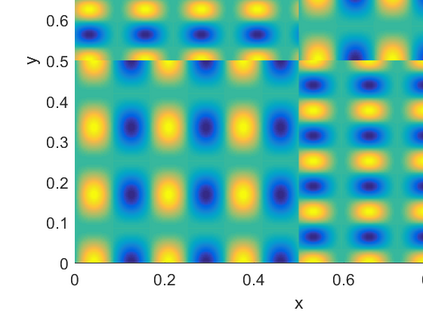
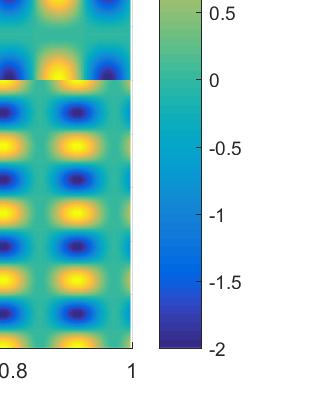
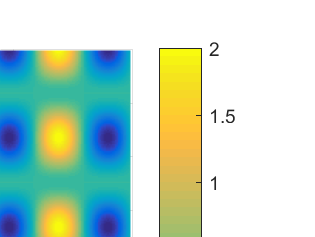
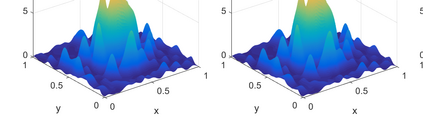
The semiclassical Schr\"odinger equation with time-dependent potentials is an important model to study electron dynamics under external controls in the mean-field picture. In this paper, we propose two multiscale finite element methods to solve this problem. In the offline stage, for the first approach, the localized multiscale basis functions are constructed using sparse compression of the Hamiltonian operator at the initial time; for the latter, basis functions are further enriched using a greedy algorithm for the sparse compression of the Hamiltonian operator at later times. In the online stage, the Schr\"odinger equation is approximated by these localized multiscale basis in space and is solved by the Crank-Nicolson method in time. These multiscale basis have compact supports in space, leading to the sparsity of stiffness matrix, and thus the computational complexity of these two methods in the online stage is comparable to that of the standard finite element method. However, the spatial mesh size in multiscale finite element methods is $ H=\mathcal{O}(\epsilon) $, while $H=\mathcal{O}(\epsilon^{3/2})$ in the standard finite element method, where $\epsilon$ is the semiclassical parameter. By a number of numerical examples in 1D and 2D, for approximately the same number of basis, we show that the approximation error of the multiscale finite element method is at least two orders of magnitude smaller than that of the standard finite element method, and the enrichment further reduces the error by another one order of magnitude.
翻译:半古典的 Schr\\" 标记方程式, 具有基于时间的潜能值, 是研究平均场景外部控制下电子动态的重要模型 。 在本文中, 我们提出两种多尺度的限定元素方法来解决这个问题 。 在离线阶段, 第一个方法是使用汉密尔顿操作员在初始阶段的稀薄压缩来构建本地化的多尺度基函数; 对于后者, 基函数将使用一种贪婪的算法来进一步丰富。 在网络阶段, Schr\" 标签方程式在空间中由这些本地化的多尺度基数基数近似电子动态, 并且由 Clank- Nicolson 方法及时解决 。 在离线阶段, 这些多尺度基数基数在空间中具有支持力, 导致坚硬度矩阵矩阵矩阵的宽度, 因此在网络阶段操作的计算方法中, 多尺度的最小值值值值值值为 $- mindalal 标准值为 1, 的基数为 基数的基数, 基数为 基数为 基数的 基数为 基数的基数为 基数为 级的 级的 级的 级值为 基数为 级值的 级值的基数为 级值的 级值的 级值的 级值的 级值的 级值为 级值为 。