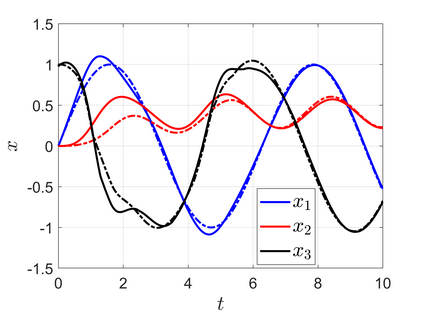
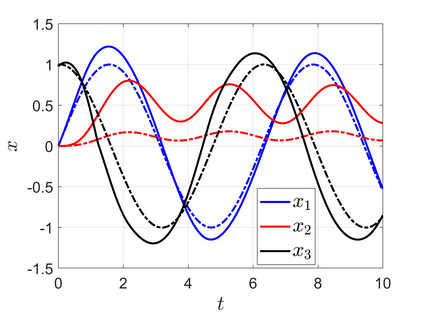
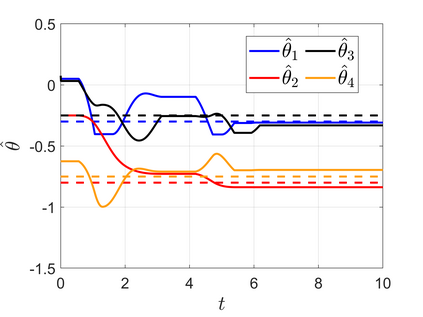
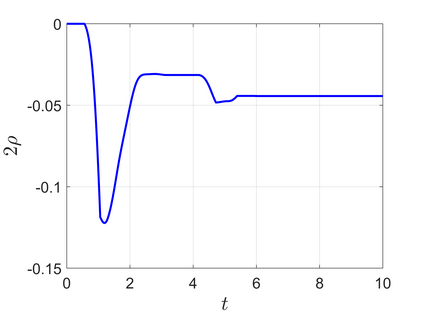
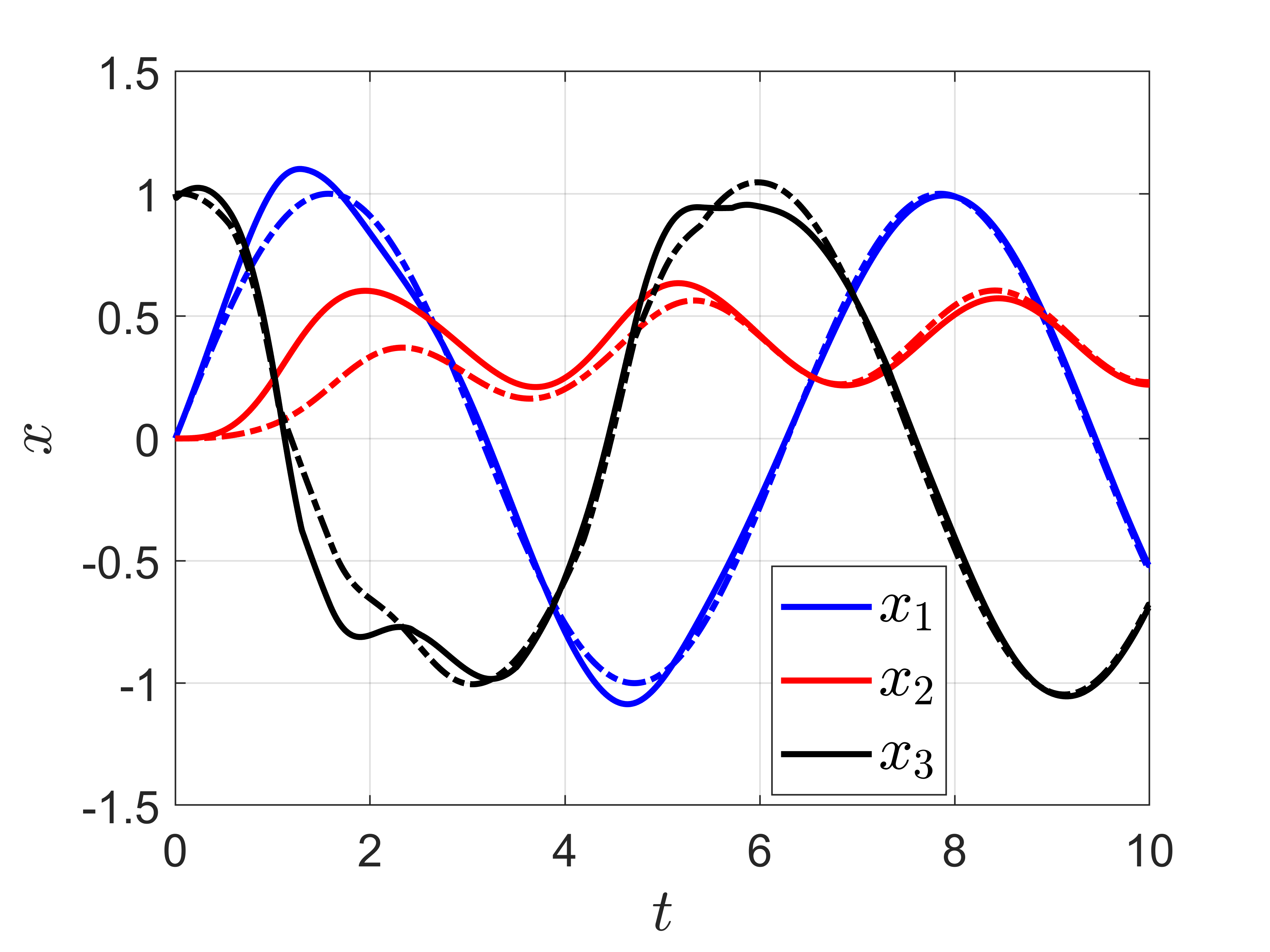
High-performance feedback control requires an accurate model of the underlying dynamical system which is often difficult, expensive, or time-consuming to obtain. Online model learning is an attractive approach that can handle model variations while achieving the desired level of performance. However, most model learning methods developed within adaptive nonlinear control are limited to certain types of uncertainties, called matched uncertainties, because the certainty equivalency principle can be employed in the design phase. This work develops a universal adaptive control framework that extends the certainty equivalence principle to nonlinear systems with unmatched uncertainties through two key innovations. The first is introducing parameter-dependent storage functions that guarantee closed-loop tracking of a desired trajectory generated by an adapting reference model. The second is modulating the learning rate so the closed-loop system remains stable during the learning transients. The analysis is first presented under the lens of contraction theory, and then expanded to general Lyapunov functions which can be synthesized via feedback linearization, backstepping, or optimization-based techniques. The proposed approach is more general than existing methods as the uncertainties can be unmatched and the system only needs to be stabilizable. The developed algorithm can be combined with learned feedback policies, facilitating transfer learning and bridging the sim-to-real gap. Simulation results showcase the method
翻译:高性能反馈控制要求有一个基础动态系统的准确模型,这种模型往往困难、昂贵或耗时,难以获取。在线模型学习是一种有吸引力的方法,可以处理模型变异,同时达到预期的性能水平。然而,在适应性非线性控制下开发的大多数模型学习方法仅限于某些类型的不确定性,称为匹配的不确定性,因为在设计阶段可以采用确定性等值原则。这项工作开发了一个通用的适应性控制框架,通过两个关键创新,将确定性等值原则扩大到非线性系统,而非线性不确定性与非线性系统不匹配。第一个是引入基于参数的存储功能,保证对适应性参考模型生成的轨迹进行闭路跟踪。第二个是调整学习率,使封闭性环形系统在学习中保持稳定。分析首先在收缩理论的镜头下进行,然后扩展为一般Lyapunov函数,这些功能可以通过反馈线性线性、后步制或优化技术加以合成。拟议的方法比现有方法更为笼统,因为不确定性可以不匹配,而系统只需要稳定地跟踪系统所生成的轨迹轨迹轨迹。开发的算法可以与升级,可以结合学习。