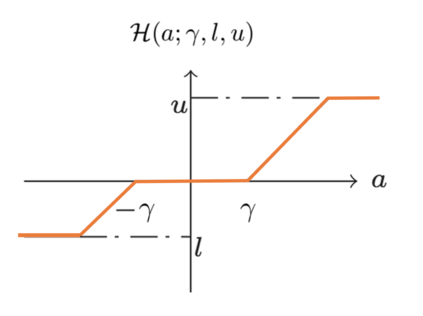
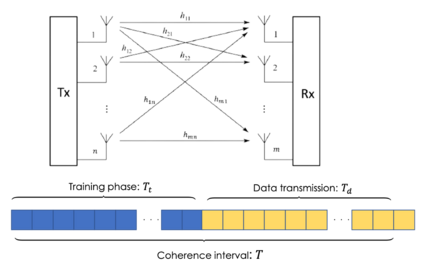
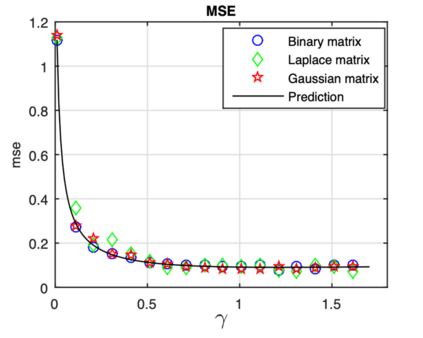
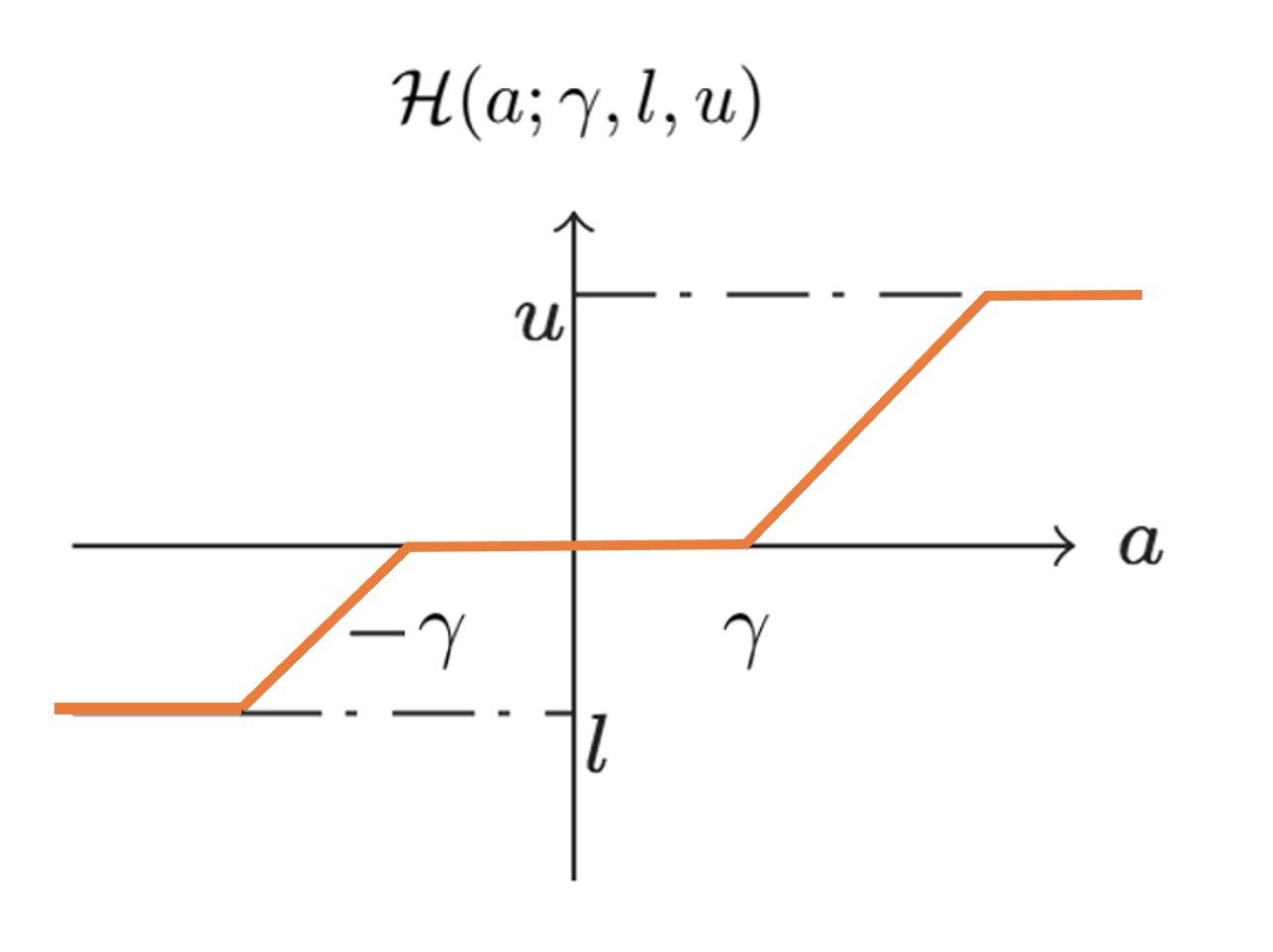
We propose in this work to employ the Box-LASSO, a variation of the popular LASSO method, as a low-complexity decoder in a massive multiple-input multiple-output (MIMO) wireless communication system. The Box-LASSO is mainly useful for detecting simultaneously structured signals such as signals that are known to be sparse and bounded. One modulation technique that generates essentially sparse and bounded constellation points is the so-called generalized space-shift keying (GSSK) modulation. In this direction, we derive high dimensional sharp characterizations of various performance measures of the Box-LASSO such as the mean square error, probability of support recovery, and the element error rate, under independent and identically distributed (i.i.d.) Gaussian channels that are not perfectly known. In particular, the analytical characterizations can be used to demonstrate performance improvements of the Box-LASSO as compared to the widely used standard LASSO. Then, we can use these measures to optimally tune the involved hyper-parameters of Box-LASSO such as the regularization parameter. In addition, we derive optimum power allocation and training duration schemes in a training-based massive MIMO system. Monte Carlo simulations are used to validate these premises and to show the sharpness of the derived analytical results.
翻译:在这项工作中,我们提议采用广受欢迎的LASSO(LASOS)方法的变异,即作为大规模多投入多输出无线通信系统的低复杂度解码器。Box-LASSO主要用于同时探测结构化信号,例如已知稀少和受约束的信号。产生基本上稀少和受约束星座点的一种调制技术是所谓的通用空控键(GSSK)调制。在这个方向上,我们得出对Box-LASO各种性能措施的高度敏锐定性,例如平均平方差、支持恢复的可能性和元素错误率,在独立和同样分布(即d.)的渠道下,这些系统并不完全为人所知。特别是,分析性能描述可用来显示Box-LASO相对于广泛使用的标准的LASSO(GSSO)调制。然后,我们可以利用这些措施对Box-LASO(GSO)的所涉超度参数进行最优化的调整,例如平均平方差差、支持恢复的概率和元素误差率率率率率率(例如,MLASO)系统所使用的最优化的模拟和最优化的模拟数据化期。此外,我们将这些模型用于模拟的模型的模型的模型的模型的模型的校正定化。