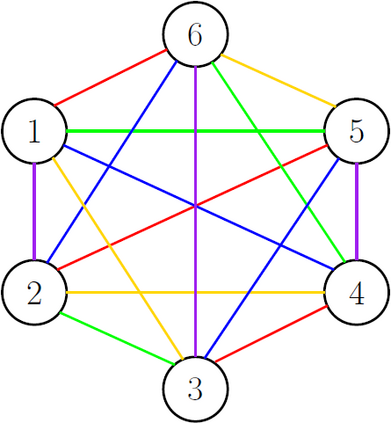
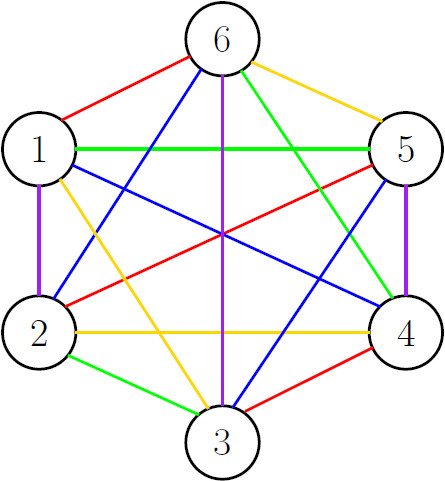
Large-scale sparse precision matrix estimation has attracted wide interest from the statistics community. The convex partial correlation selection method (CONCORD) developed by Khare et al. (2015) has recently been credited with some theoretical properties for estimating sparse precision matrices. The CONCORD obtains its solution by a coordinate descent algorithm (CONCORD-CD) based on the convexity of the objective function. However, since a coordinate-wise update in CONCORD-CD is inherently serial, a scale-up is nontrivial. In this paper, we propose a novel parallelization of CONCORD-CD, namely, CONCORD-PCD. CONCORD-PCD partitions the off-diagonal elements into several groups and updates each group simultaneously without harming the computational convergence of CONCORD-CD. We guarantee this by employing the notion of edge coloring in graph theory. Specifically, we establish a nontrivial correspondence between scheduling the updates of the off-diagonal elements in CONCORD-CD and coloring the edges of a complete graph. It turns out that CONCORD-PCD simultaneously updates off-diagonal elements in which the associated edges are colorable with the same color. As a result, the number of steps required for updating off-diagonal elements reduces from p(p-1)/2 to p-1 (for even p) or p (for odd p), where p denotes the number of variables. We prove that the number of such steps is irreducible In addition, CONCORD-PCD is tailored to single-instruction multiple-data (SIMD) parallelism. A numerical study shows that the SIMD-parallelized PCD algorithm implemented in graphics processing units (GPUs) boosts the CONCORD-CD algorithm multiple times.
翻译:大规模分散的精确矩阵估计引起了统计界的广泛兴趣。 由 Khare 等人( 2015 ) 开发的CONCORD 部分相关选择方法( CONCORD) 最近以一些理论属性被某些理论属性归功于估算稀少精确矩阵。 COCORD 以目标函数的精度为基础,通过一个协调的基底算法( CONCORD- CD) 获得其解决方案。 然而, 由于CONCORD- CD 中协调式更新本质上是序列性的, 规模提升是非边际的。 在本文中, 我们提议对CONCORD- CD (ConCORD- PCD. COCOCORD- PCD) 开发一个新颖的平行选择方法, 将非直径元素分成几个组, 并同时对每个组进行更新。 我们保证, 在图形理论理论理论中, 将边端颜色- CORD- 和 直径变量的边端值排序。