Optimal homotopy reconstruction results à la Niyogi, Smale, and Weinberger

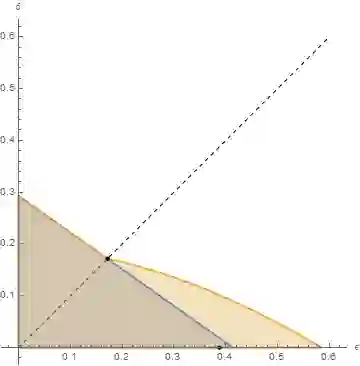
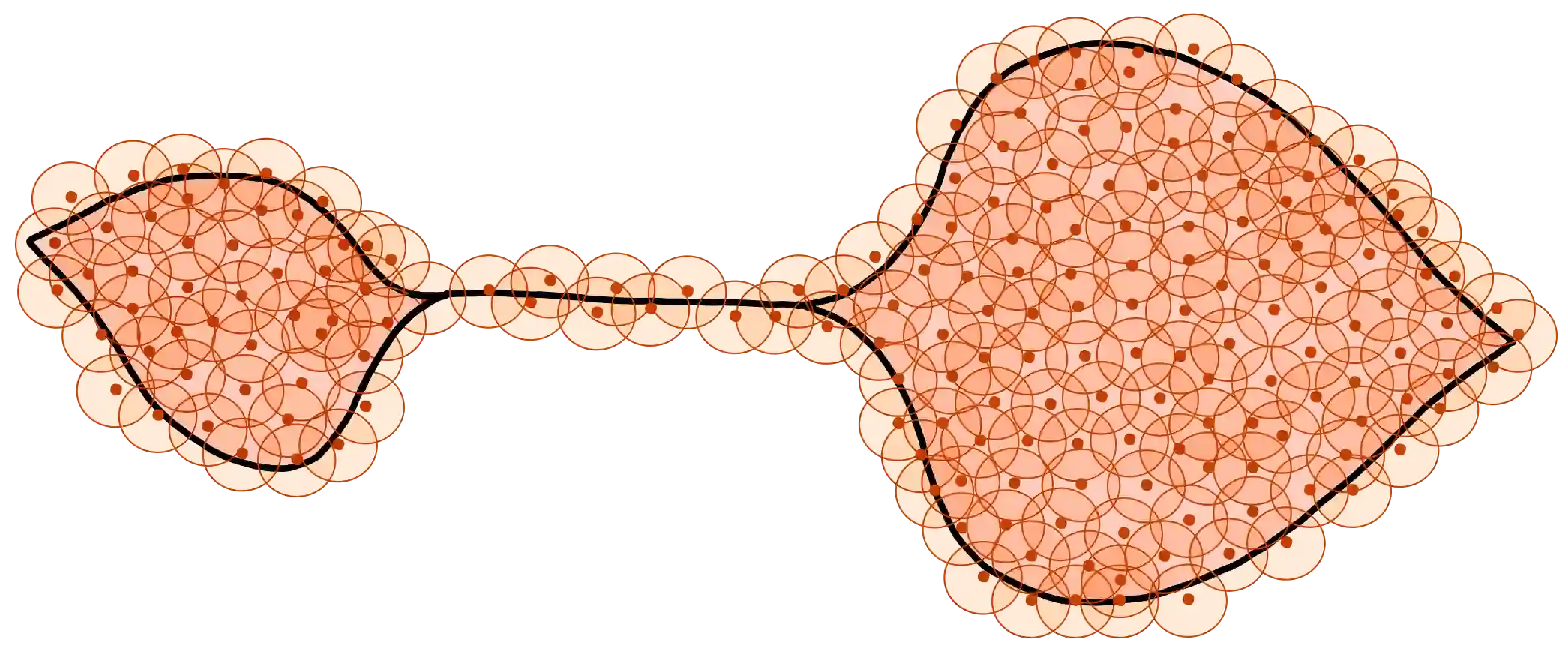
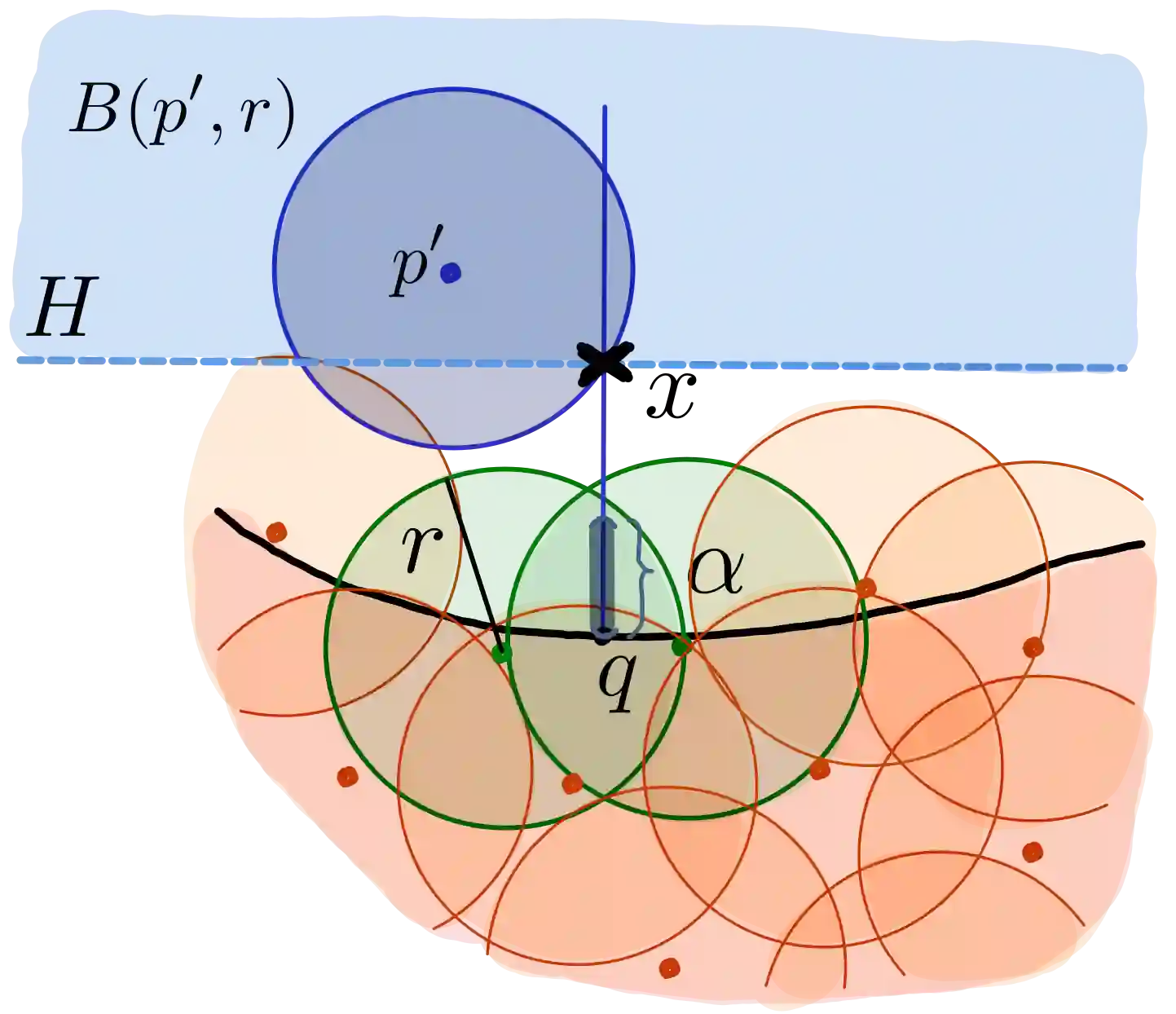
In this article we show that the proof of the homotopy reconstruction result by Niyogi, Smale, and Weinberger can be streamlined considerably using Federer's work on the reach and several geometric observations. While Niyogi, Smale, and Weinberger restricted themselves to C2 manifolds with positive reach, our proof extends to sets S of positive reach. The sample we consider does not have to lie directly on the set of positive reach. Instead, we assume that the two one-sided Hausdorff distances (delta and epsilon) -- between the sample P to the set S, are bounded. We provide explicit bounds in terms of epsilon and delta, that guarantee that there exists a parameter r such that the union of balls of radii r centered on the points of the sample P deformation retracts to S. We provide even better bounds for the manifold case. In both cases, our bounds improve considerably on the state-of-the-art in almost all settings. In fact the bounds are optimal.