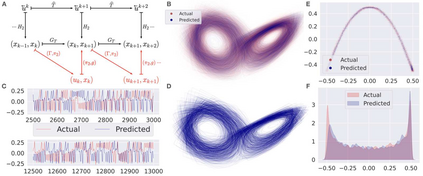
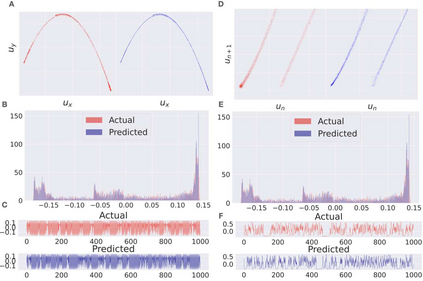
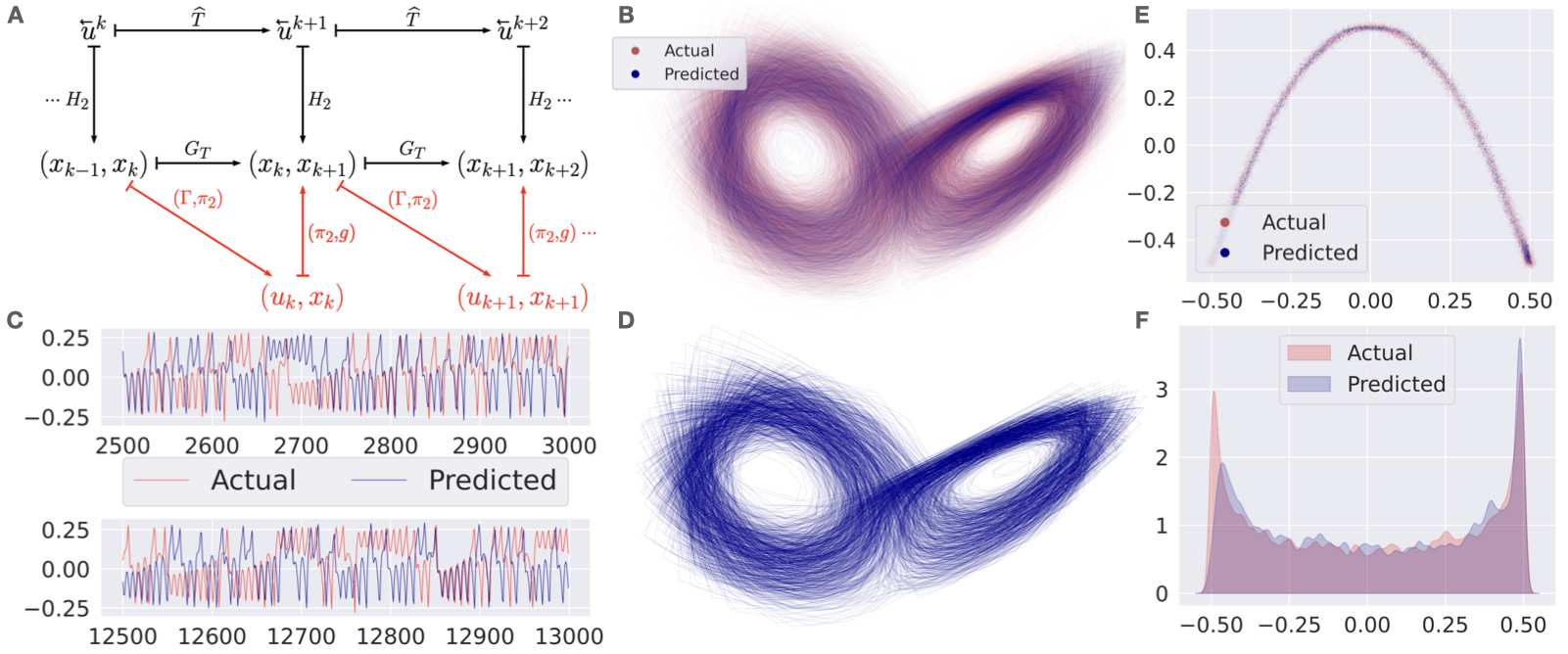
Obtaining repeated measurements through observables of underlying physical and natural systems to build dynamical models is engraved in modern science. A key to the success of such methods is that the dynamics in the observed space can often be described by a map that has much lower functional complexity than the one that describes the unknown underlying system. Finding observables that can empirically reduce the functional complexity of the map to be learned, and at the same time, theoretically guarantee exact reconstruction in the new phase space is an open challenge. Here, we determine a set of observables for the Koopman operator of the inverse-limit system of a dynamical system that guarantees exact reconstruction of the underlying dynamical system. Similar to the delay coordinate maps being universal observables in Takens delay embedding, the observables we determine are universal, and hence do not need to be changed while the underlying system is changed. They are determined by a class of driven systems that are comparable to those used in reservoir computing, but which also can causally embed a dynamical system, a phenomenon which we newly describe. Dynamics in the observed space is then shown to be topologically conjugate to the underlying system. Deep learning methods can be used to learn accurate equations from data as a consequence of the topological conjugacy. Besides stability, amenability for hardware implementations, causal embedding-based models provide long-term consistency even for systems that have failed with previously reported data-driven or machine learning methods.
翻译:通过对基本物理和自然系统进行观测以建立动态模型的反复测量,在现代科学中被刻画了。这种方法成功的关键是,观测空间的动态常被描述为功能复杂性远低于描述未知基础系统的地图。找到能够从经验上减少地图功能复杂性的观测,同时,理论上保证在新阶段空间进行精确重建是一个公开的挑战。在这里,我们为一个动态系统反向限制系统的库普曼操作员确定了一系列观测结果,该动态系统保证了基础动态系统的确切重建。类似地,所观测空间的动态动态动态动态系统动态动态的动态可被描述为在使用延迟嵌入时普遍观测的地图,我们确定的观测结果是普遍性的,因此在改变基础系统时不需要改变。这些观测结果是由一类驱动系统所决定的,这种系统与储油层计算所使用的系统相仿,但也可能因果性地嵌入一个动态系统,一种我们新描述的现象。观测到的空间动态动态动态系统随后显示,从表学角度将地图与基础系统相连接起来。我们确定的动态系统是,因此,我们确定的观察结果是:在延迟嵌嵌入后,我们确定一个精确的机型数据流化的模型,因此,可以使用一种数据流数据流数据流化的计算方法可以用来学习一个精确度,可以用来学习一个硬化的硬性模型,而使用。