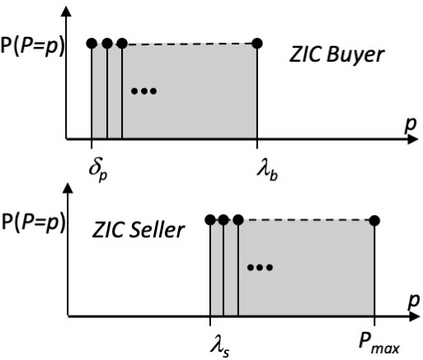
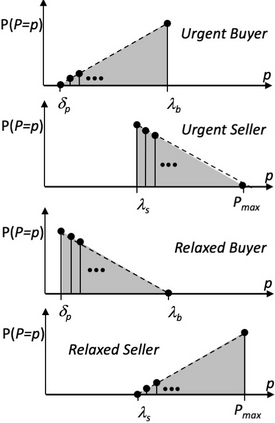
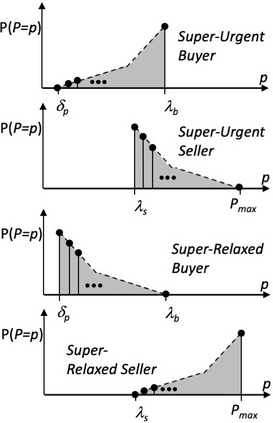
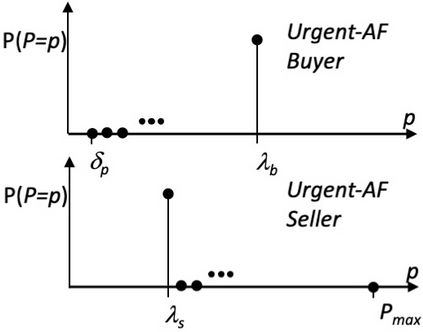
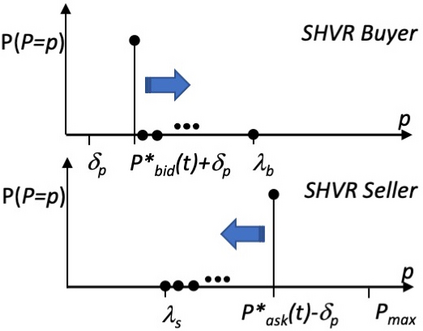
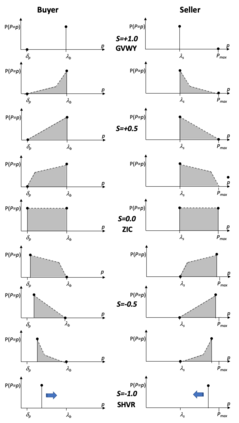
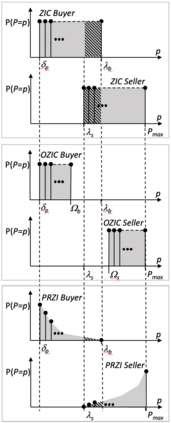
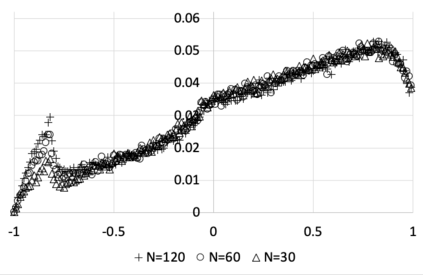
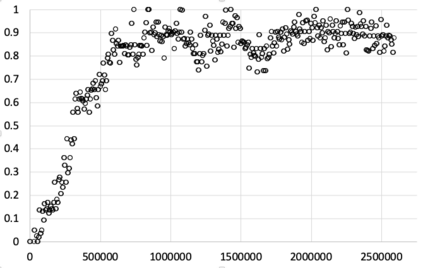
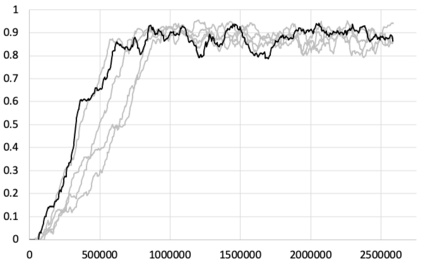
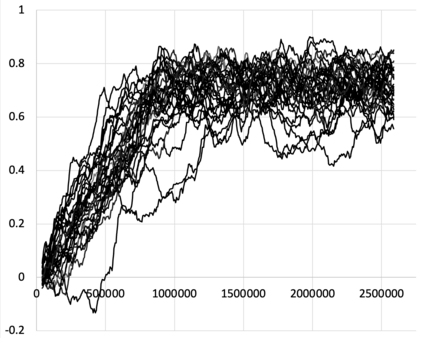
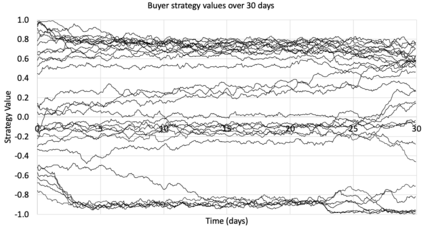
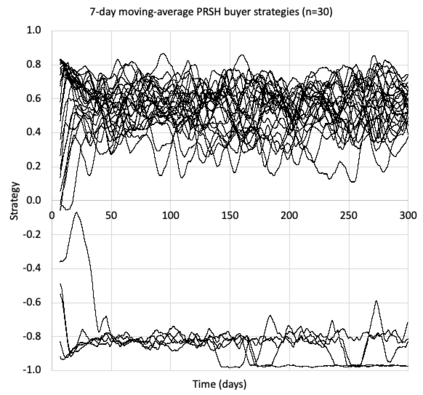
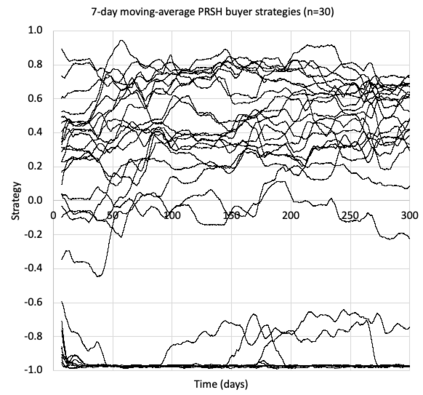
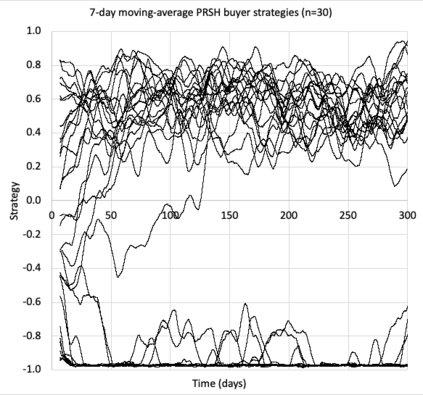
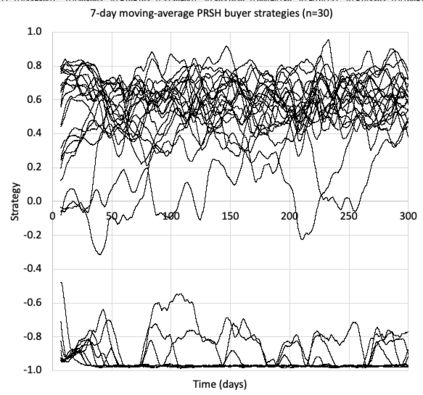
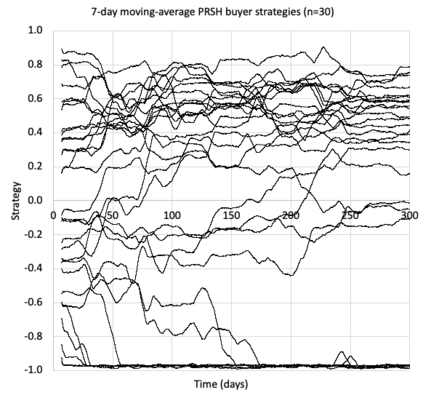
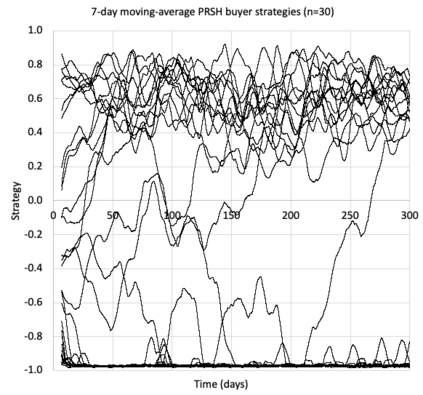
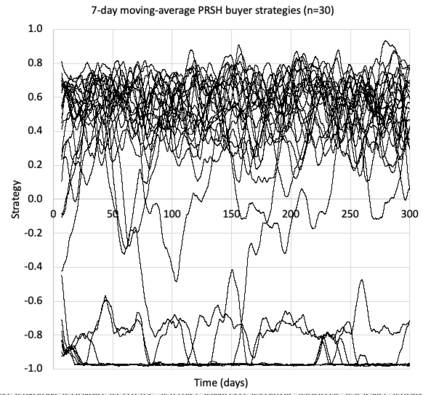
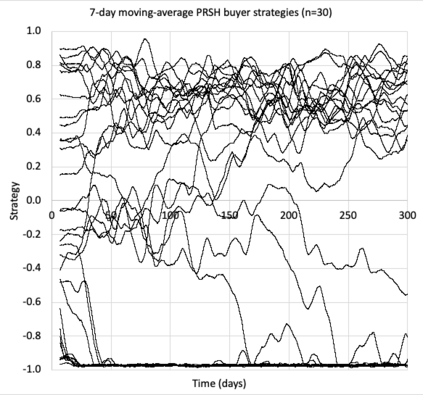
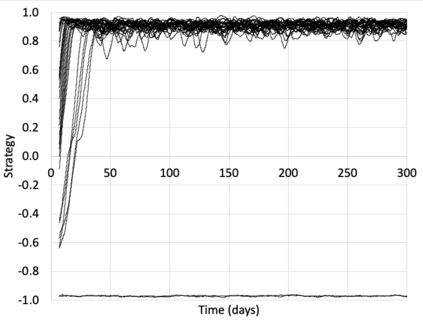
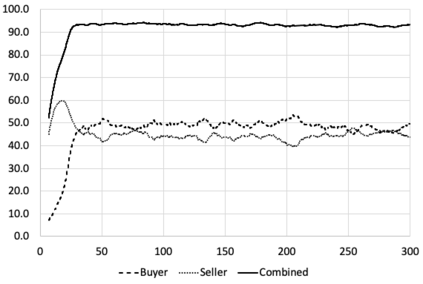
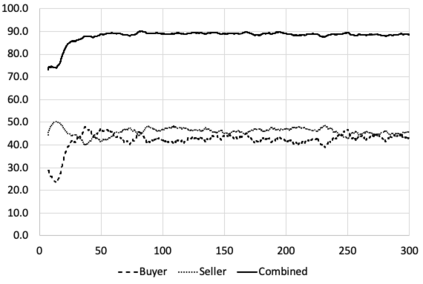
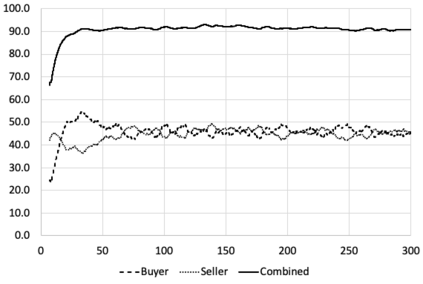
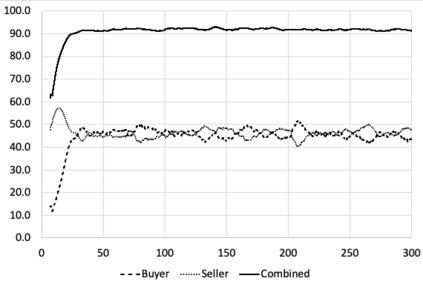
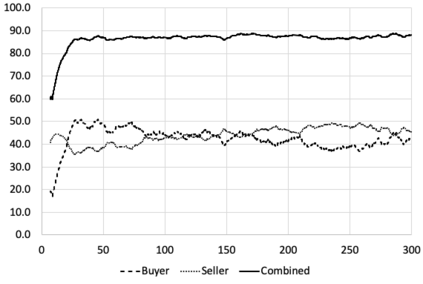
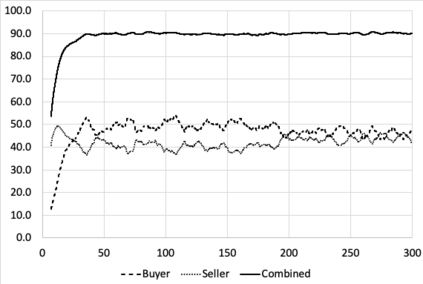
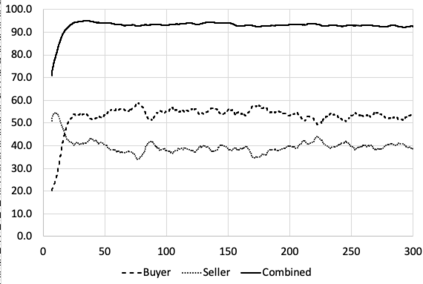
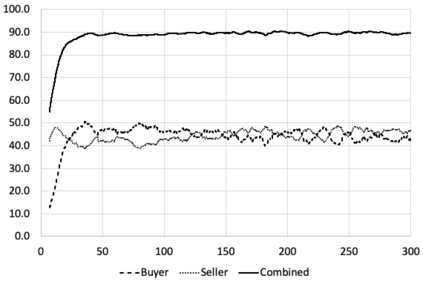
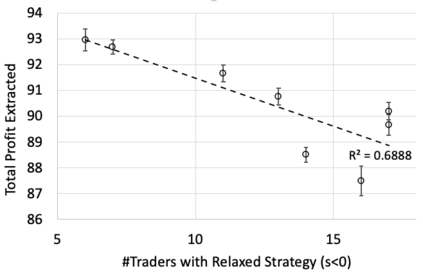
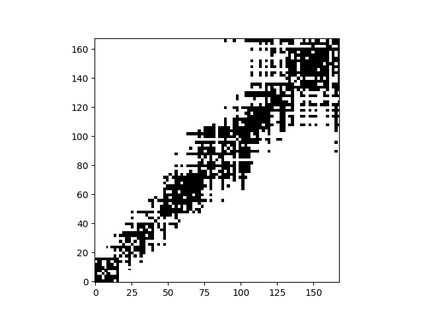
I introduce PRZI (Parameterised-Response Zero Intelligence), a new form of zero-intelligence trader intended for use in simulation studies of the dynamics of continuous double auction markets. Like Gode & Sunder's classic ZIC trader, PRZI generates quote-prices from a random distribution over some specified domain of allowable quote-prices. Unlike ZIC, which uses a uniform distribution to generate prices, the probability distribution in a PRZI trader is parameterised in such a way that its probability mass function (PMF) is determined by a real-valued control variable s in the range [-1.0, +1.0] that determines the _strategy_ for that trader. When s=0, a PRZI trader is identical to ZIC, with a uniform PMF; but when |s|=~1 the PRZI trader's PMF becomes maximally skewed to one extreme or the other of the price-range, thereby making its quote-prices more or less urgent, biasing the quote-price distribution toward or away from the trader's limit-price. To explore the co-evolutionary dynamics of populations of PRZI traders that dynamically adapt their strategies, I show results from long-term market experiments in which each trader uses a simple stochastic hill-climber algorithm to repeatedly evaluate alternative s-values and choose the most profitable at any given time. In these experiments the profitability of any particular s-value may be non-stationary because the profitability of one trader's strategy at any one time can depend on the mix of strategies being played by the other traders at that time, which are each themselves continuously adapting. Results from these market experiments demonstrate that the population of traders' strategies can exhibit rich dynamics, with periods of stability lasting over hundreds of thousands of trader interactions interspersed by occasional periods of change. Python source-code for the work reported here has been made publicly available on GitHub.
翻译:我引入了一种新型的零情报交易员, 用于模拟连续双重拍卖市场动态的研究。 像 Gode & Sunder 的经典 ZIC 交易员一样, PRZI 从某些特定允许报价域的随机分配中产生报价。 与 ZIC 不同的是, PZI 交易员使用统一分配来产生价格, PRZI 交易员的概率分布被参数化了, 其概率质量功能是由一个在范围[- 1.0, +1.0] 上的真实价值控制变量决定的。 这决定了该交易员的汇率。 当 s=0, PRZI 交易员的报价价格是同ZIC 一样的, 而 PZI 交易员的PMF 最有可能被一个极端或另一个价格等级的汇率扭曲, 从而使得其价格更加紧迫, 偏偏向或偏向另一个不同的价格交易额, 交易员的汇率分布在交易员的直径或偏向或偏向一个不同的交易员, 交易员的汇率战略在交易时值上不断调整。
相关内容
Source: Apple - iOS 8