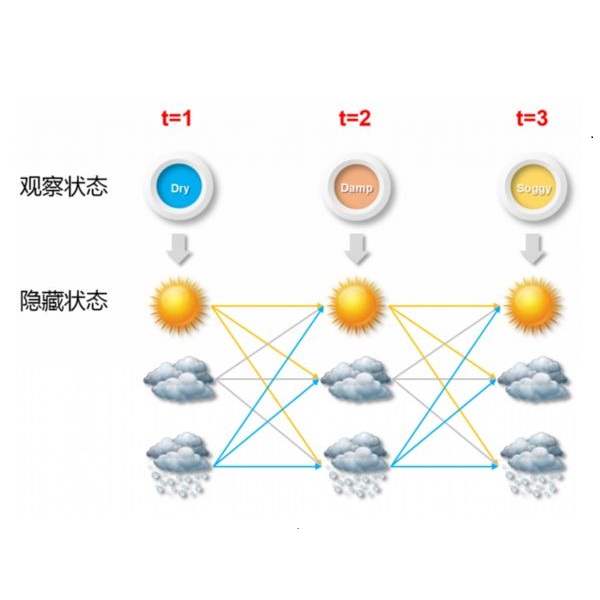
We propose to model time-varying periodic and oscillatory processes by means of a hidden Markov model where the states are defined through the spectral properties of a periodic regime. The number of states is unknown along with the relevant periodicities, the role and number of which may vary across states. We address this inference problem by a Bayesian nonparametric hidden Markov model assuming a sticky hierarchical Dirichlet process for the switching dynamics between different states while the periodicities characterizing each state are explored by means of a trans-dimensional Markov chain Monte Carlo sampling step. We develop the full Bayesian inference algorithm and illustrate the use of our proposed methodology for different simulation studies as well as an application related to respiratory research which focuses on the detection of apnea instances in human breathing traces.
翻译:我们建议通过一个隐蔽的马尔科夫模型来模拟时间变化周期和螺旋过程,该模型通过周期制度的光谱特性来界定各州。国家的数量与相关周期并不清楚,其作用和数量可能因州而异。我们处理巴伊西亚非对称隐蔽的马尔科夫模型的推论问题,该模型假定不同州之间转换动态的粘性等级分级分解过程,而每个州特征的周期性则通过一个跨维的马尔科夫链蒙卡洛取样步骤来探索。我们开发了完整的巴耶西亚推论算法,并说明了我们为不同模拟研究以及侧重于探测人类呼吸痕迹中的脉搏现象的呼吸研究应用而提出的方法。