有力的推断 (Powerful Inference)

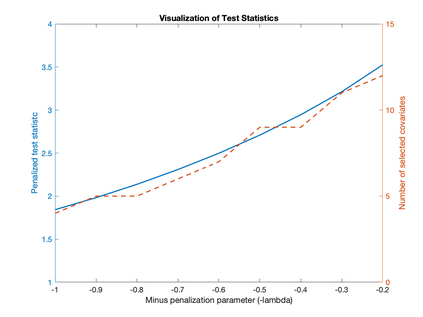
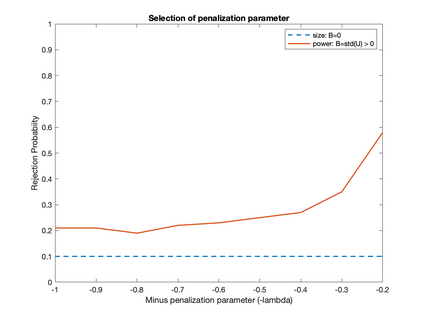
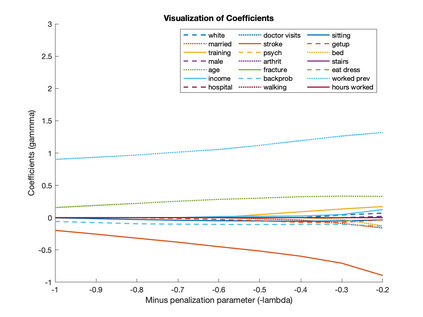
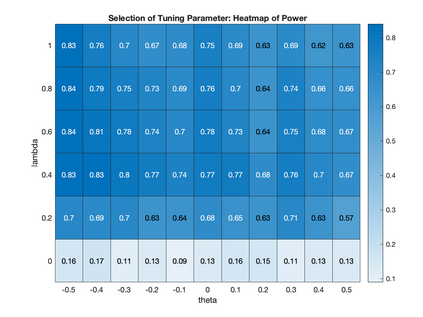
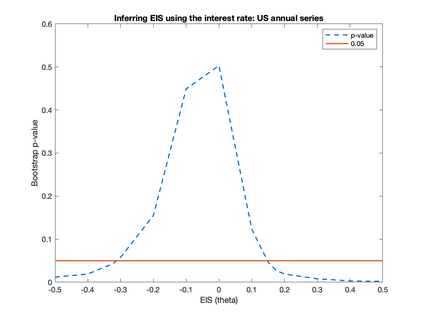
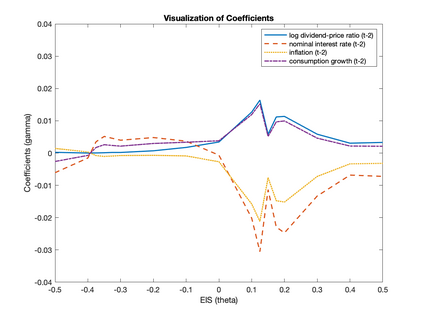
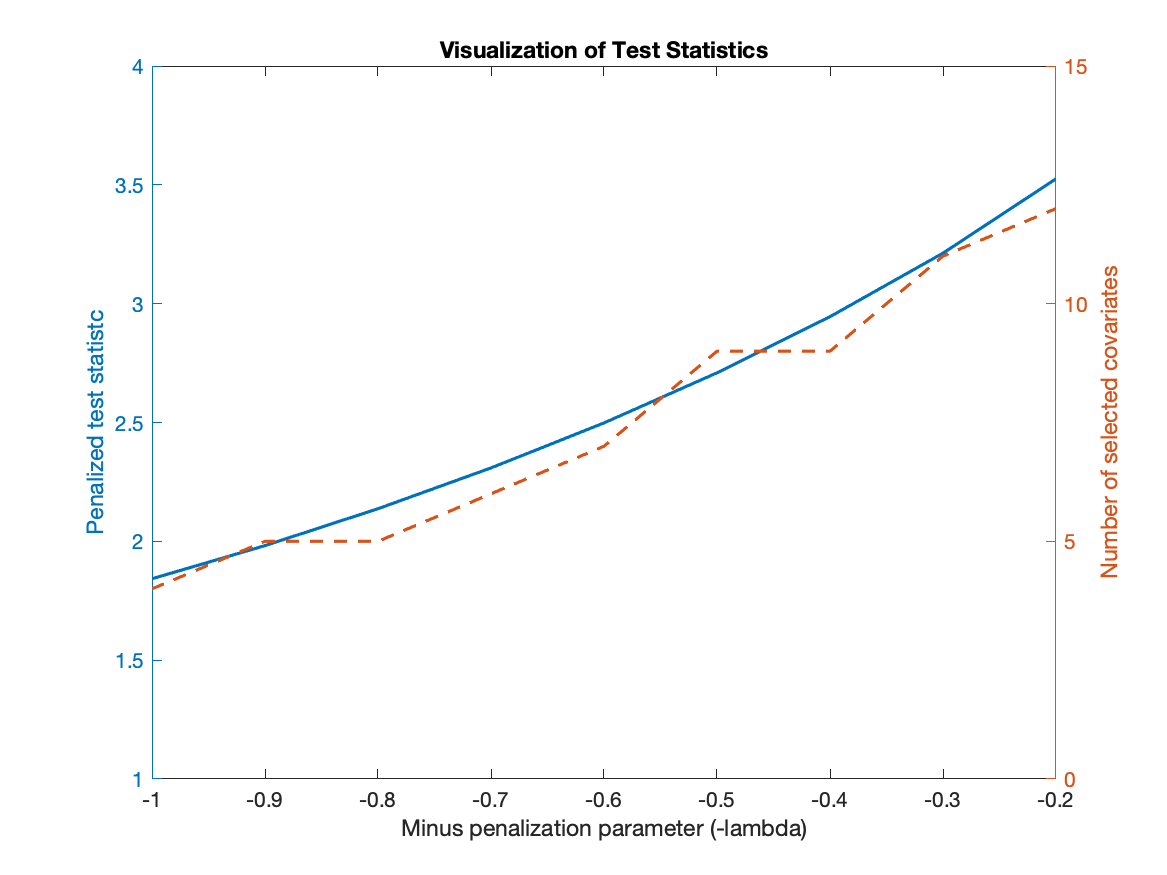
We develop an inference method for a (sub)vector of parameters identified by conditional moment restrictions, which are implied by economic models such as rational behavior and Euler equations. Building on Bierens (1990), we propose penalized maximum statistics and combine bootstrap inference with model selection. Our method is optimized to be powerful against a set of local alternatives of interest by solving a data-dependent max-min problem for tuning parameter selection. We demonstrate the efficacy of our method by a proof of concept using two empirical examples: rational unbiased reporting of ability status and the elasticity of intertemporal substitution.

翻译：我们为有条件时间限制确定的参数(子)的推论者制定了一种(子)推论方法,这是理性行为和Euler等方程式等经济模型所隐含的。在Bierens(1990年)的基础上,我们提出惩罚性最高统计数字,并将靴带推论与模型选择结合起来。我们的方法最优化,通过解决数据依赖最大限度的参数选择问题,对一套当地利益替代物发挥强大的作用。我们用两个经验性例子(合理公正地报告能力状况和时际替代的弹性)来证明我们的方法的有效性。我们用两个经验性例子来证明我们的方法的有效性:合理公平地报告能力状况和时际替代的弹性。