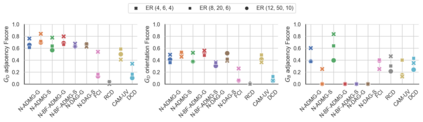
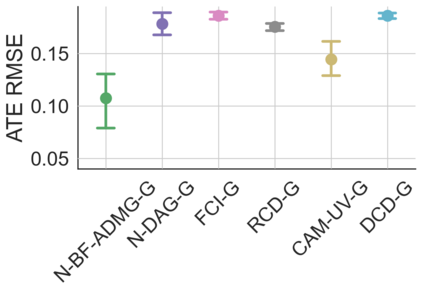
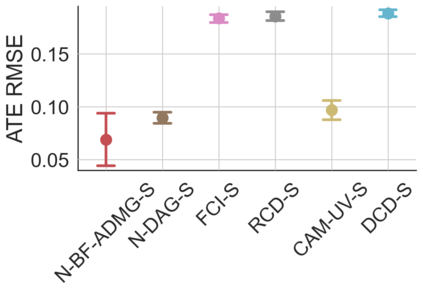
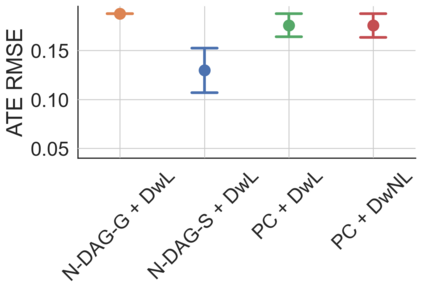
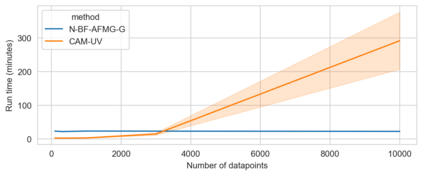
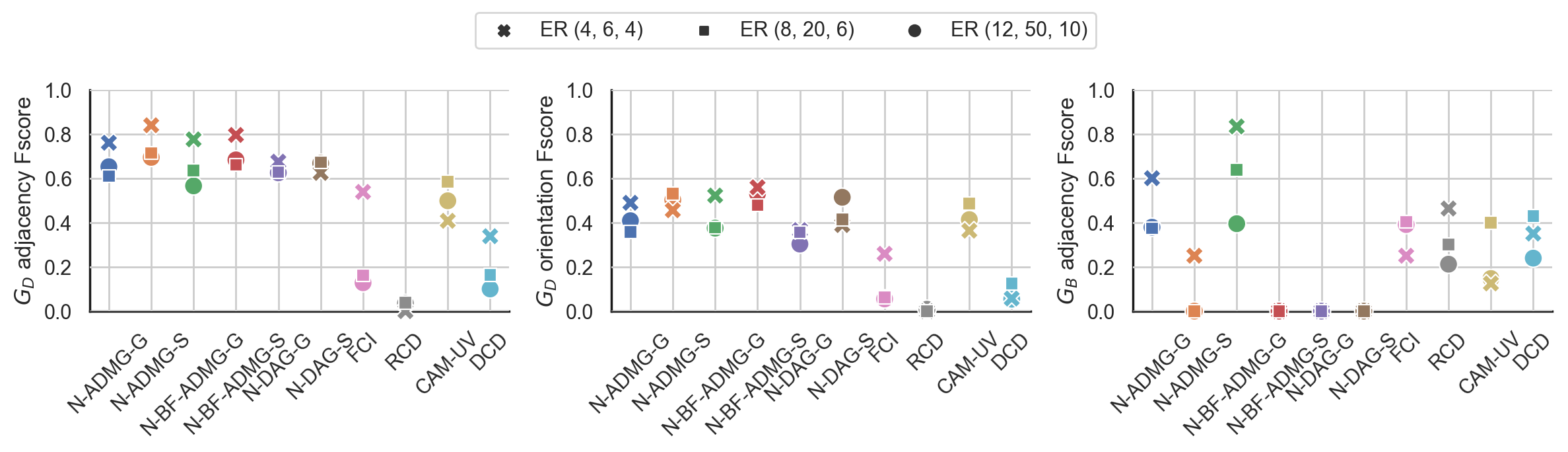
Latent confounding has been a long-standing obstacle for causal reasoning from observational data. One popular approach is to model the data using acyclic directed mixed graphs (ADMGs), which describe ancestral relations between variables using directed and bidirected edges. However, existing methods using ADMGs are based on either linear functional assumptions or a discrete search that is complicated to use and lacks computational tractability for large datasets. In this work, we further extend the existing body of work and develop a novel gradient-based approach to learning an ADMG with non-linear functional relations from observational data. We first show that the presence of latent confounding is identifiable under the assumptions of bow-free ADMGs with non-linear additive noise models. With this insight, we propose a novel neural causal model based on autoregressive flows for ADMG learning. This not only enables us to determine complex causal structural relationships behind the data in the presence of latent confounding, but also estimate their functional relationships (hence treatment effects) simultaneously. We further validate our approach via experiments on both synthetic and real-world datasets, and demonstrate the competitive performance against relevant baselines.
翻译:Translated abstract:
潜在混淆一直是从观察数据进行因果推理的长期障碍。一种流行的方法是使用无环有向混合图(ADMG),它使用定向和双向边描述变量之间的祖先关系。然而,现有的ADMG方法基于线性函数假设或者是复杂的离散搜索,对于大型数据集缺乏计算可处理性。在本研究中,我们进一步扩展现有的工作,从观察数据中开发一种基于非线性函数关系的ADMGS学习的新型基于梯度的方法。我们首先表明,在ADMGS的无弓形假定和非线性附加噪声模型的情况下,存在潜在混淆是可辨识的。基于此,我们提出了一种新的基于自回归流程的神经因果模型,用于ADMGS学习。这不仅可以使我们在存在潜在混淆的数据背后确定复杂的因果结构关系,同时还可以同时估计它们的函数关系(因此是治疗效果)。我们通过对合成数据和真实世界数据集的实验进一步验证了我们的方法,并展示了与相关基线的竞争性能。